Hossein M. Shodja


Professor, Department of Civil Engineering and Institute for Nanoscience and Nanotechnology, Sharif University of Technology, Tehran, Iran
Fellow, American Society of Mechanical Engineers (ASME)
General Intrest: Mechanics and Materials
Research Associate, Theoretical and Applied Mechanics, Northwestern University, Evanston, IL, USA.
Postdoctoral Fellow, Theoretical and Applied Mechanics, Northwestern University, Evanston, IL, USA.
Ph.D., Theoretical and Applied Mechanics, Northwestern University, Evanston, IL, USA.
M.Sc., Applied Mathematics, Michigan State University, East Lansing, MI, USA.
M.Sc., Civil Engineering (Solid Mechanics), Michigan State University, East Lansing, MI, USA.
B.Sc., Civil Engineering (Structural Mechanics), Michigan State University, East Lansing, MI, USA.
Current research works include • Various problems in the field of theoretical and applied mechanics, particularly, Nano/Micro-scale modeling of defects in ultra-small objects and thin films via atomistic approaches, augmented continuum theories, and micromechanical considerations, capturing the surface and size effects • Ab initio calculations of the characteristic lengths of the crystalline materials in first and second strain gradient elasticity • Micromechanical based theories for the prediction of the overall behavior of elastic solids with high concentration of multi-phase particles as well as calculations of the effective moduli of nano-composites based on higher order theories • Employment of the combined analytical and first principles calculations based on density functional theory to study the mechanical behavior of carbon nano-tubes • The inverse problem of the identification of the shape and position of embedded nan-/micro- inhomogeneities from limited far-field measurments.
A precise evaluation of the numerical values of the elastic constants pertinent to polar and gradient theories in the realm of the experimentations poses serious difficulties - in this effort capture of the discrete nature of matter is an essential factor. To remedy the encountered dilemma, we have developed some theoretical methods for accurate measurements of such parameters. Theoretically determined the surface energy, surface stress, and surface elastic constants of ideal and reconstructed surfaces via combined first principles and analytical treatments. Recently, determined the micromorphic elastic constants theoretically in terms of the atomic force constants and lattice parameters of the crystalline solid with general anisotropy. Furthermore, employed weakly nonlocal micromorphic elasticity for diamond structures vis-á-vis lattice dynamics to capture not only all the acoustic branches but also all the optical branches of the dispersion curves for non-Bravais crystals like diamond and silicon over the entire first Brillouin zone.
One of the special interests is the basic research in the development of theorems associated with the multi-inclusions, multi-inhomogeneities (with anisotropic constituents), and impotent eigenstrains which are of fundamental importance in the study of micromechanics of defects in solids. These theorems are concerned with the prediction of the exact nature of the elastic fields within the constituent phases of a multi-inhomogeneous inclusion and its surrounding matrix under general far-field loading. Introduction of such innovative viewpoints of equivalent inclusion method (EIM) as the spectral EIM for rigorous and exact determination of the elastic fields; introduction of the notion of eigenbody-force fields needed for a sound basis of the dynamic EIM (DEIM). Moreover, extension of the concept of eigenstrain to the atomistic level in the atomistic study of thin-films; relation between eigenstrain and potential function suitable for accounting for the short and long range inter-atomic interactions. Development of a unified approach for determination of the closed-form expressions for modes I, II and III stress intensity factors at the tips of lamellar inhomogeneities under a remote applied polynomial loading based on Eshelby's EIM.
In addition to the analytical treatments, development of innovative computational methods such as gradient reproducing kernel particle method (GRKPM) and generalized RKPM are of interest; employment of GRKPM to such highly nonlinear partial differential equations as Burger's equation and Buckley-Leverett's equation which are characterized by exhibition of steep moving fronts.
Chemistry of Crack Initiation in Amorphous Silicon
Stress vs. true strain under both the relaxed and unrelaxed conditions. The snapshots of the electronic charge distribution show the transformation of the unstable sp3 hybridized orbital associated with the trigonal prism (b) to the stable sp2 hybridized orbital (c). The necking in one of the bonds in (b) is evident. (d) A snapshot of two reconstructed surfaces at final rupture, and (e) the structural geometry for (c).
Read moreGap Tuning in Amorphous Silicon
The electronic DOS of the strained a-Si under ϵ33 = 0.070, 0.140, and 0.210. The details of the mobility gap region for the cases of ϵ33 = 0.070, 0.140, and 0.210 are also depicted. For ϵ33 = 0.070 the midgap states are observed.
Read moreAtomistic Simulation of Crack Growth
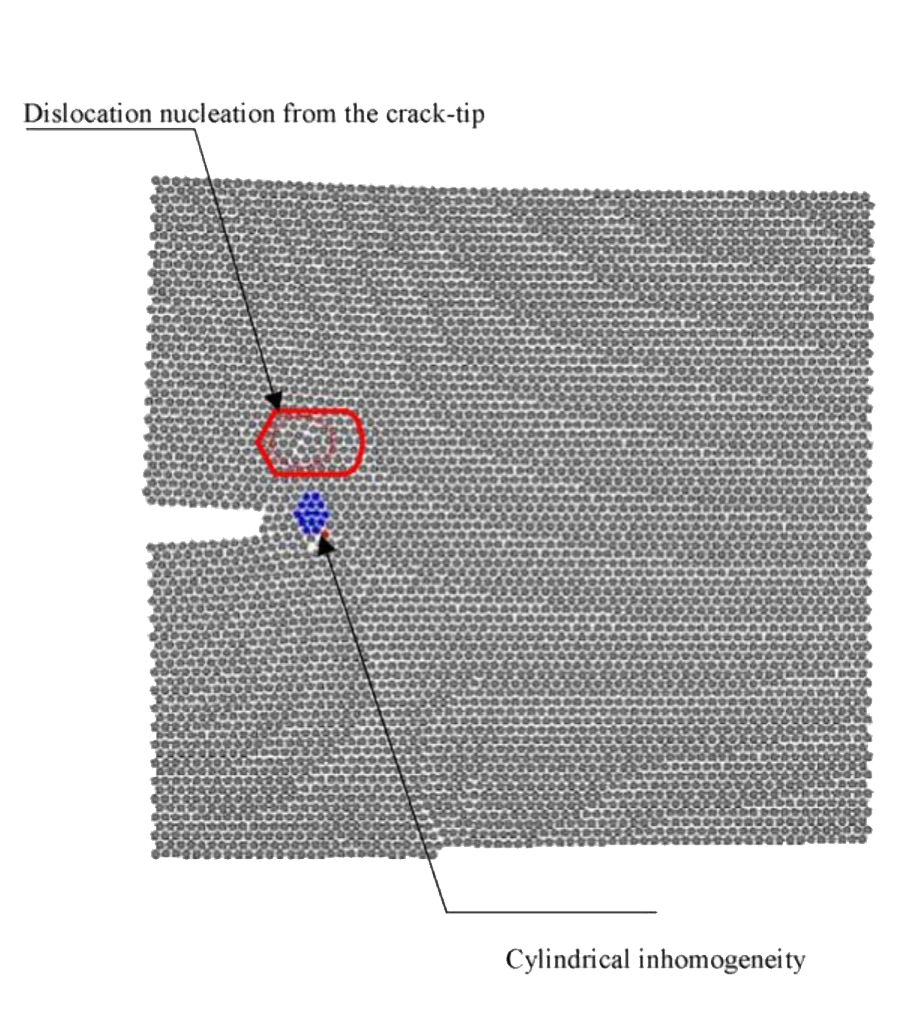
Cylindrical Cu impurity in an Ag plate. Crack stops at a distance of 3d from the impurity and dislocations are emitted.
Read more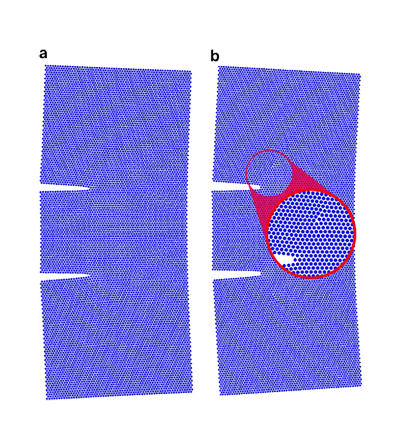
Ductile crack growth of two edge cracks of length 20d with aseparation distance of 39 atomic layers (a) before, and (b) after dislocationemission.
Read moreLarge Deformation Problems (Elastica)
2D Materials
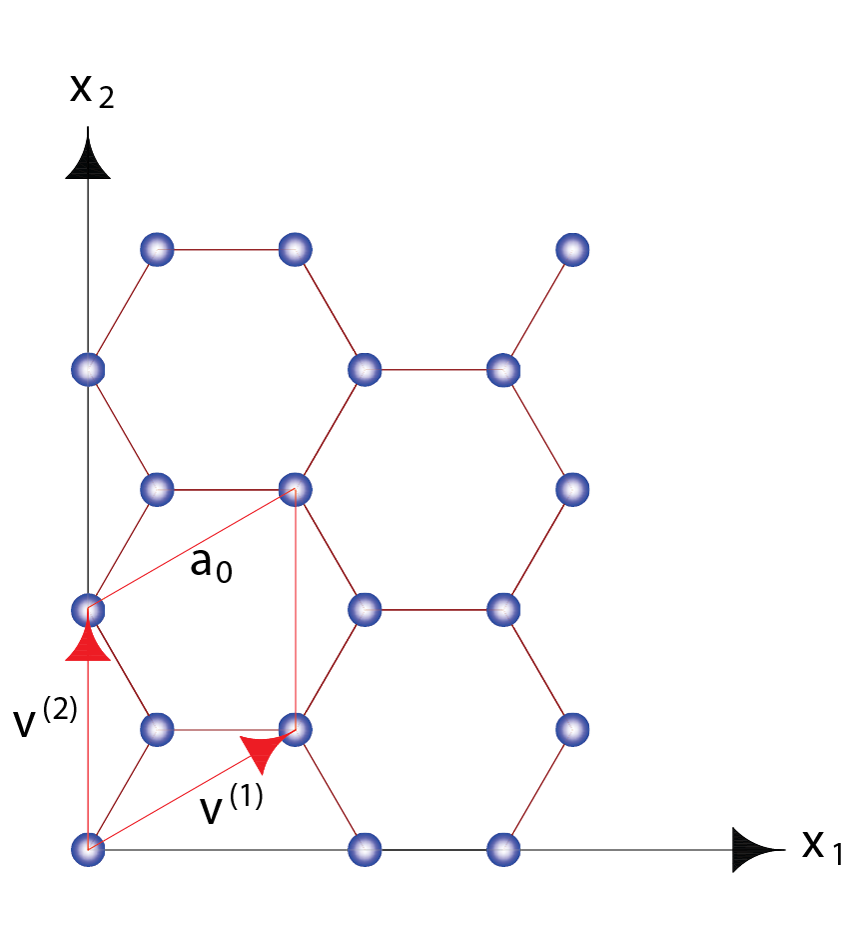
The atomic structure of stanene and the corresponding in-plane lattice vectors, ν1 and ν2 and lattice parameter, a0. AC- and ZZ-directions of the monolayer coincide with x1 and x2 axes, respectively. The two-atomic rhomboid unit cell formed by the lattice vectors ν1 and ν2 is shown.
Read more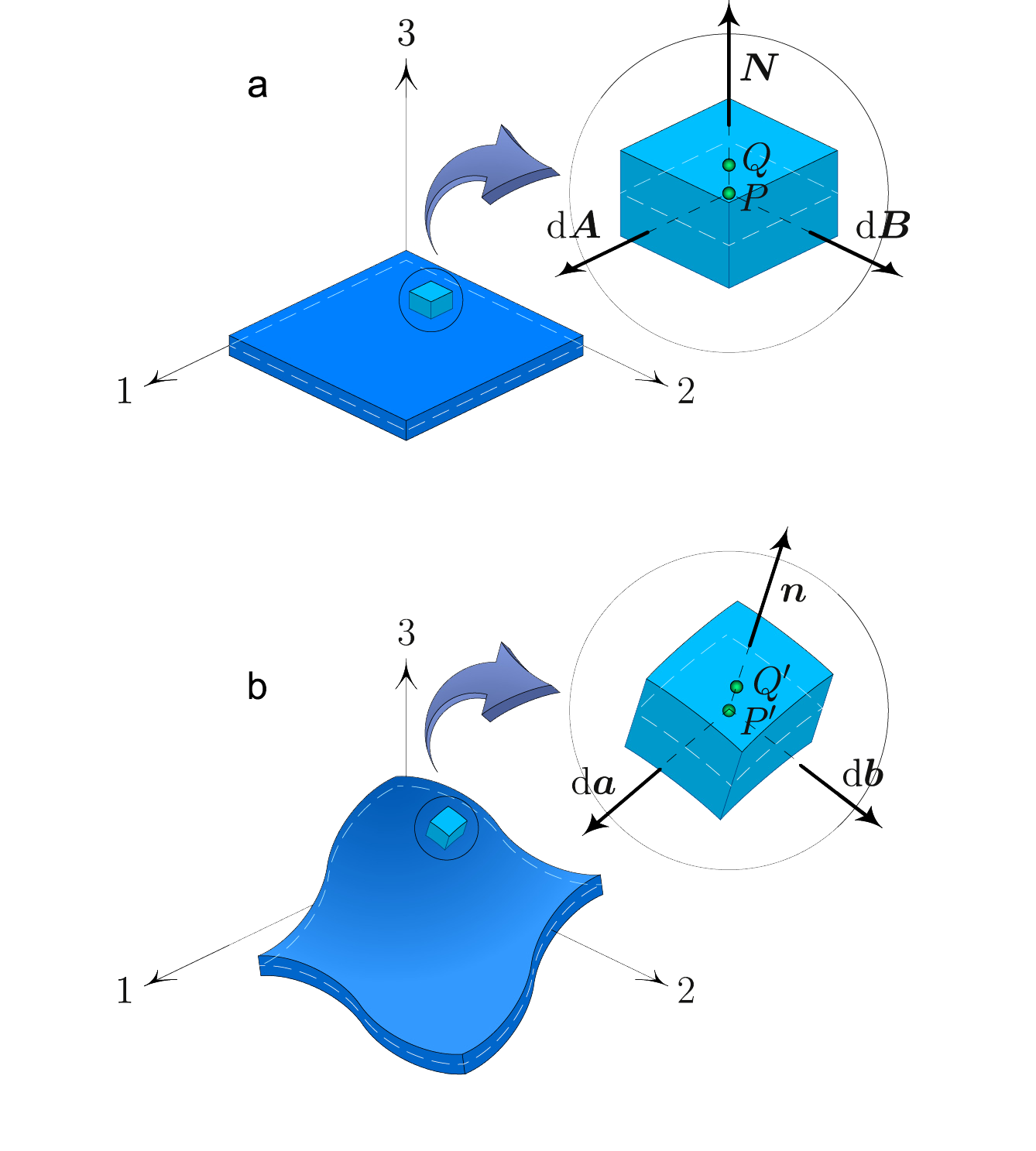
A thin plate (a) before, and (b) after deformation. After deformation, the material point Q and its projection P onto the middle surface, respectively, move to Q' and P'. dA and dB are the infinitesimal vectors at P along the 1- and 2-axis, respectively. These vectors are, respectively, transformed to da and db which are tangent to the deformed middle surface at P'.
Read moreCarbon Nanotubes
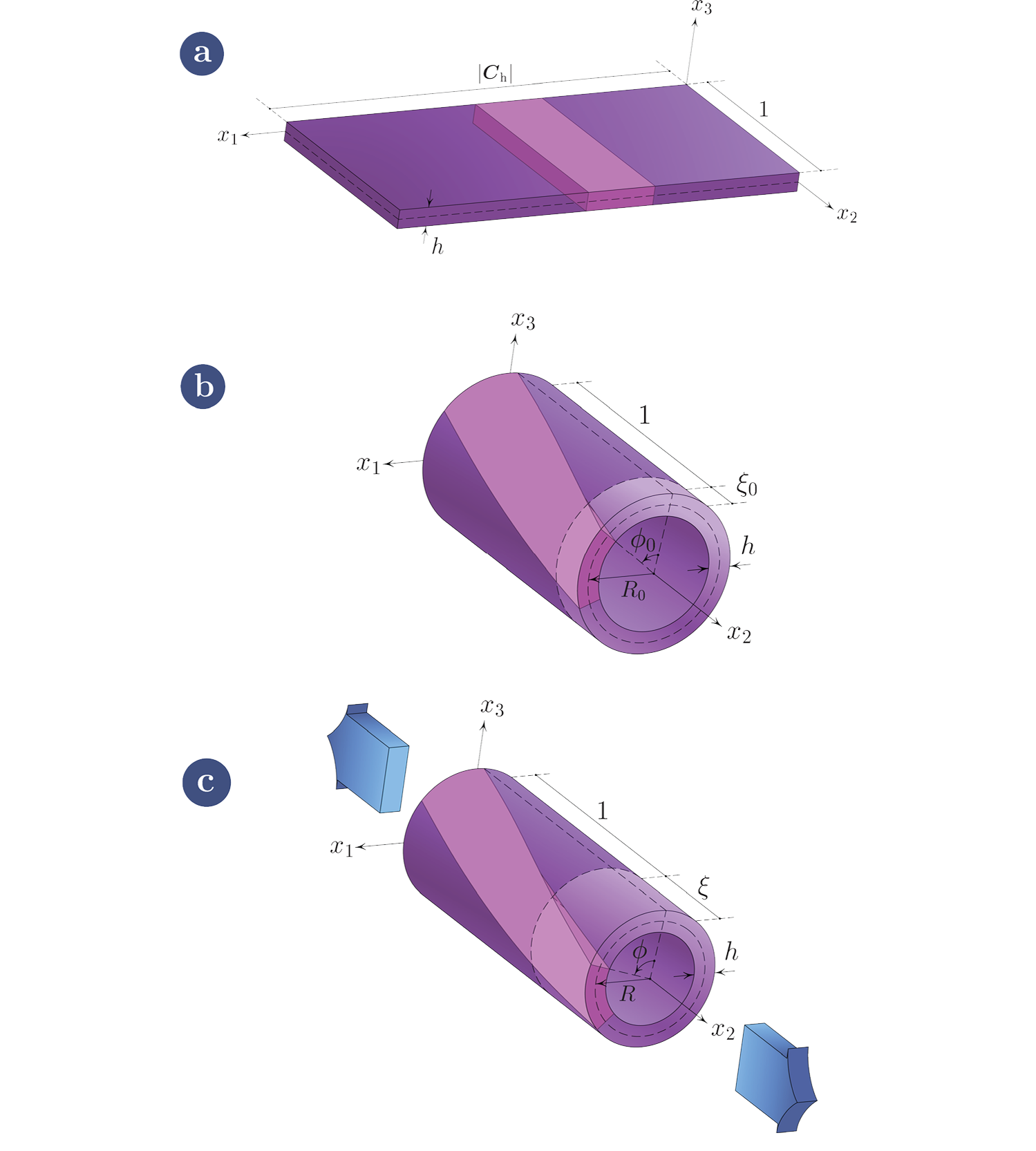
Geometry of a graphene sheet and the elastica: (a) a unit strip of graphene sheet, (b) the free-standing SWCNT, and (c) the SWCNT under axial tension.
Read moreTheoretical evaluation of the constitutive parameters of ...
(ab inition DFT; atomistic modelling; lattice dynamics)
Surface Elasticity
First Strain Gradient Elasticity
Second Strain Gradient Elasticity
Inverse Nano-inhomogeneity Problems
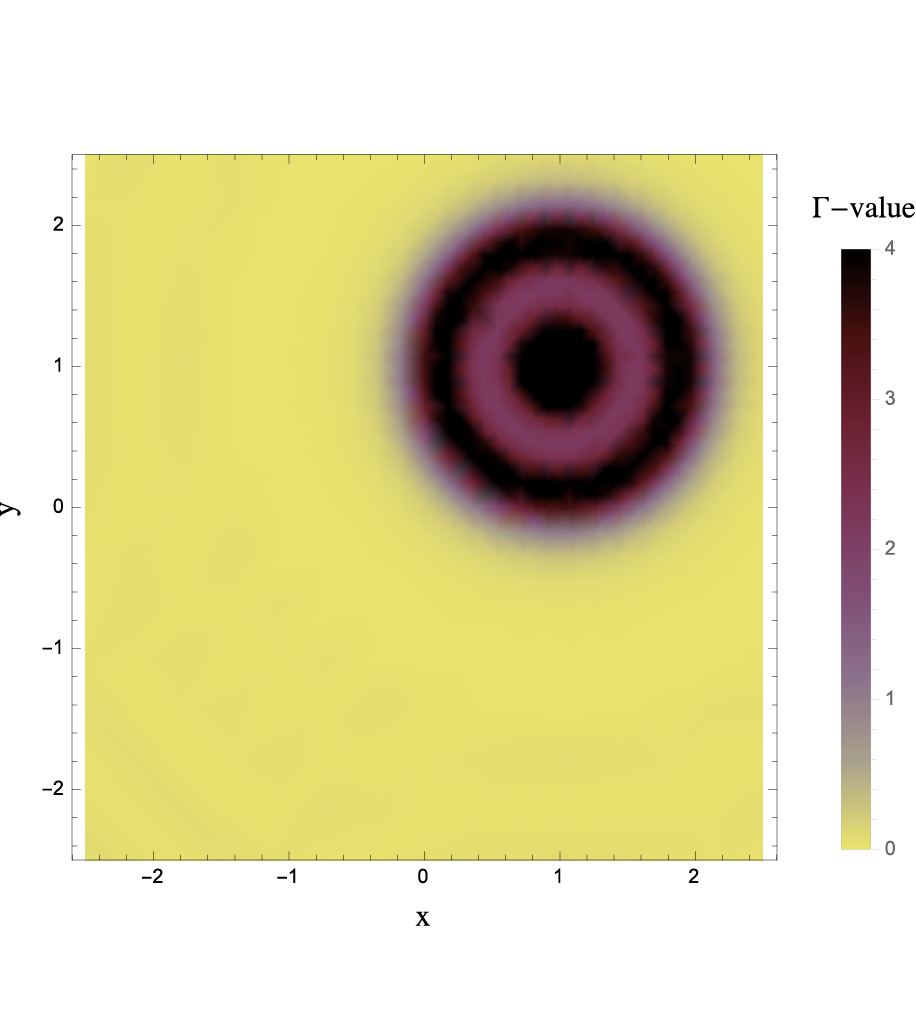
Density plots of the indicator function, Γ associated with the reconstruction of the size and location of a rigid, micro-/nano-fiber with radius 1 located at (√ 2 , π/4).
Read moreWave Propagation
Mechanical Waves with Surface Effects
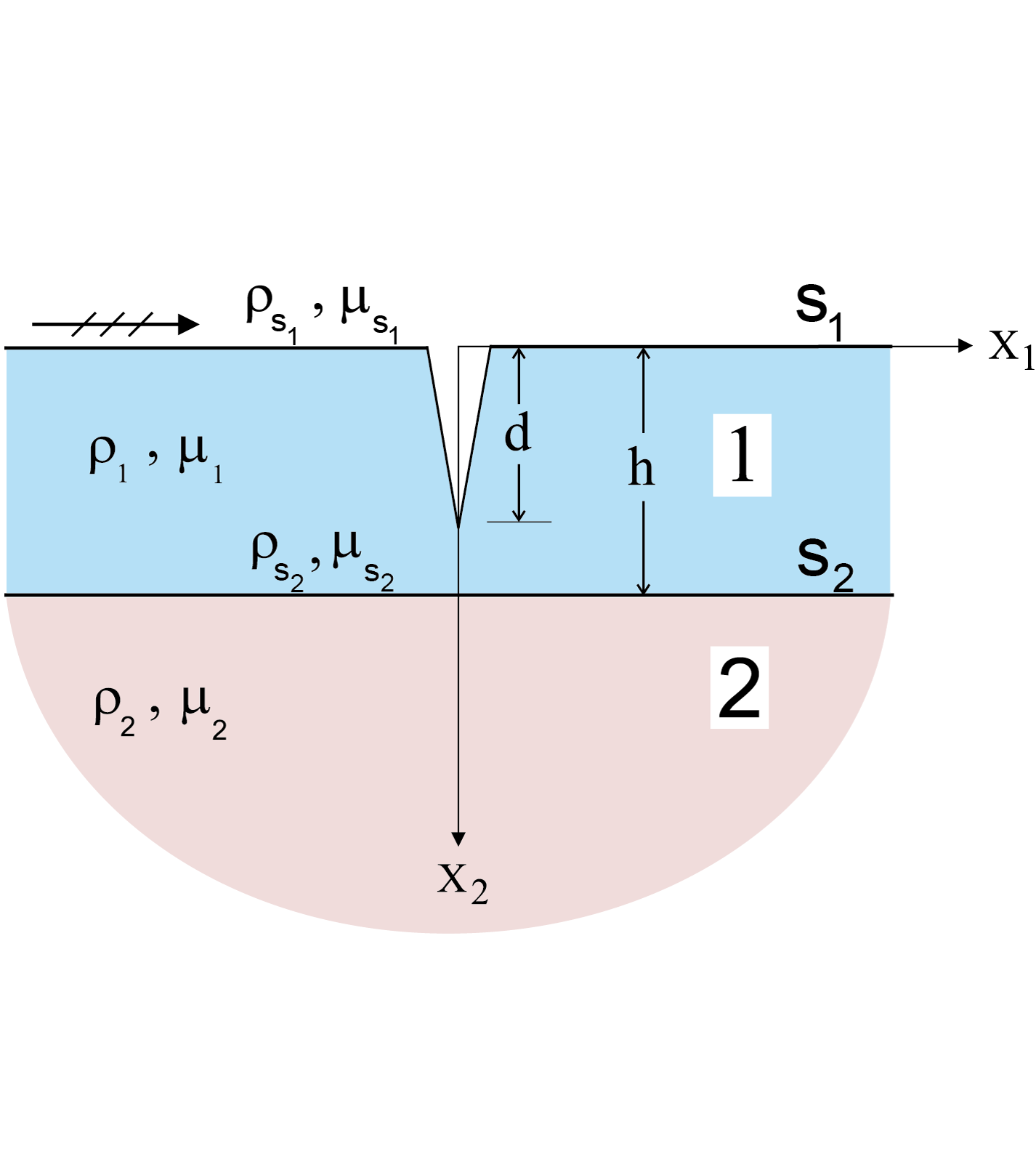
Love wave propagating in a thin layer-substrate system. Wave is incident on a nano-size surface breaking crack contained within the layer.
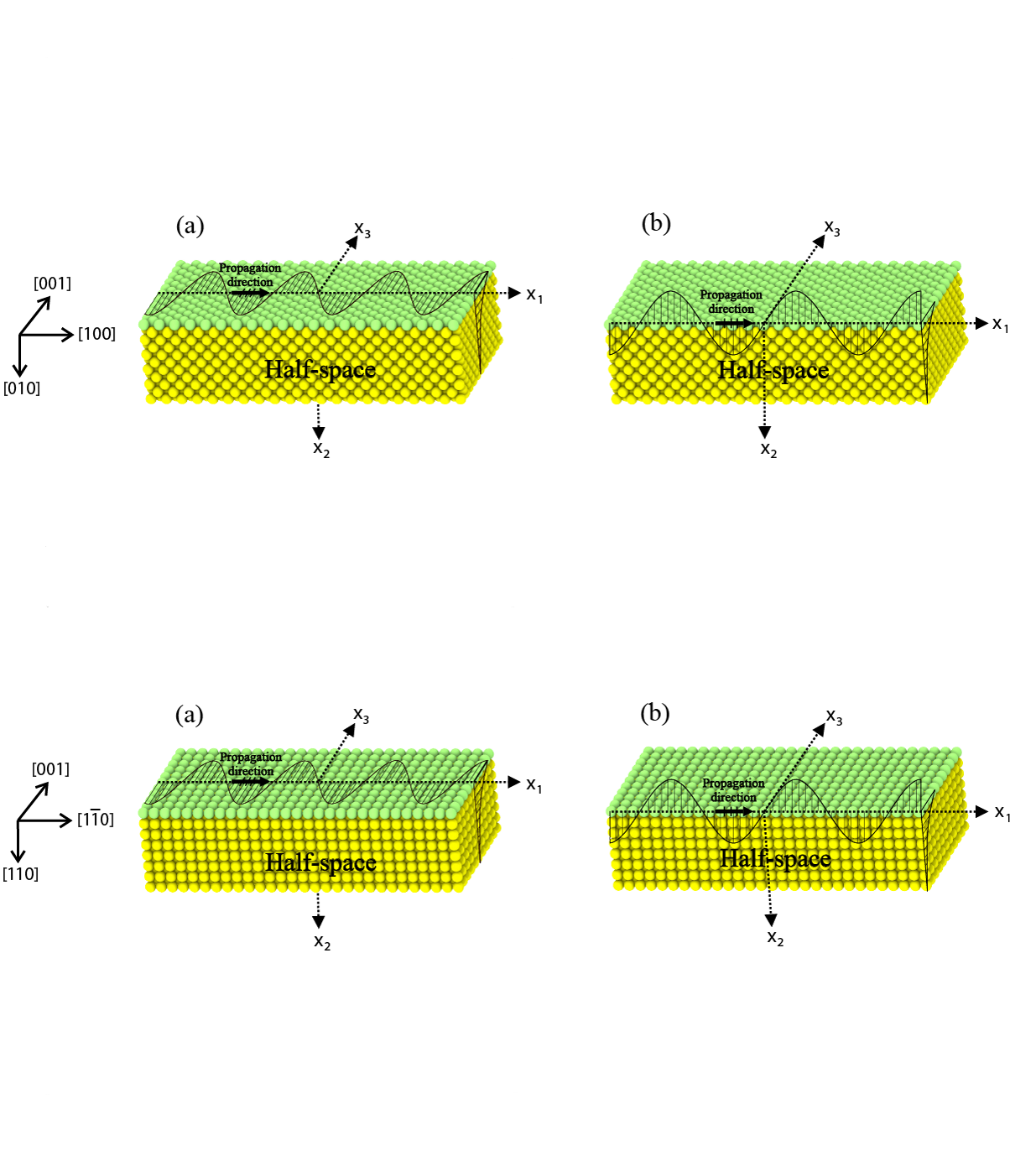
(a) Love and (b) Rayleigh Surface wave propagation in a half-space with free surface.
Mechanical Waves within Couple Stress Theory with Micro-inertia
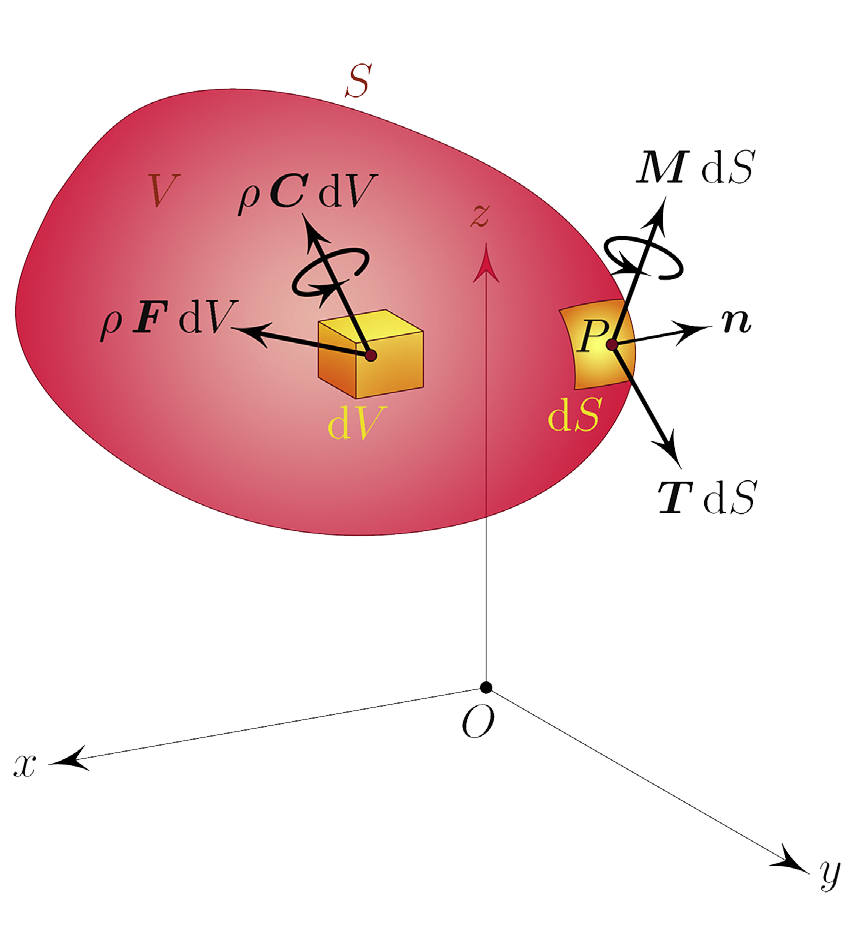
The free body diagram of an arbitrary macro-element with volume, V and surface S. n is the unit outward normal to S. q is the mass density, r is the spatial position, dV is the volume of the micro-element or unit cell and dS is the elemental area. T, M, F, and C denote surface stress, couple stress, body force, and body couple, respectively.
Scattering of Mechanical Waves by Eccentric Multi-phase Scatterers
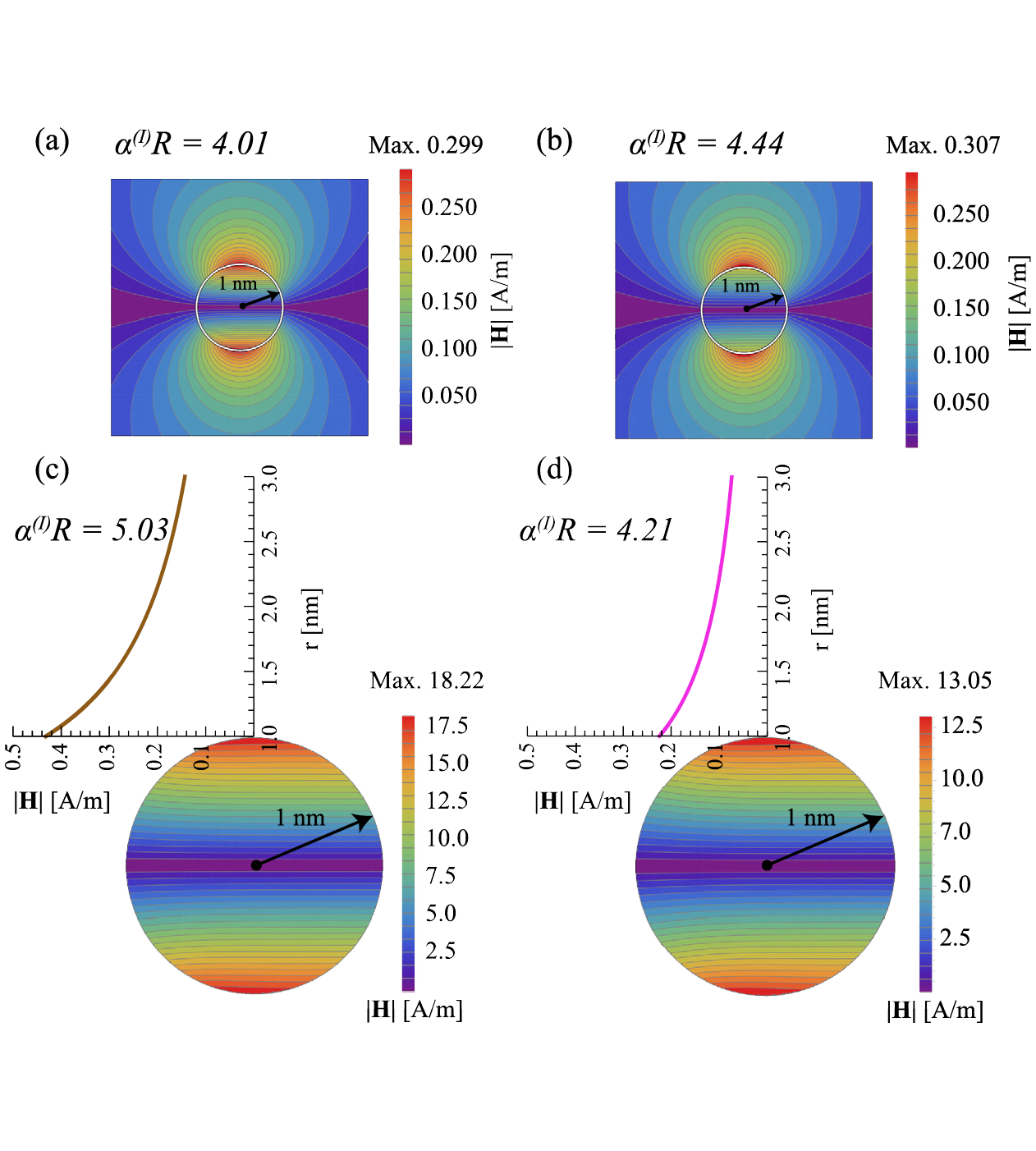
The distribution of the magnetic field: (a) classical, (b), (c), and (d) non-classical, respectively, corresponding to the different interface conditions.
Theoretical Developements in Micromechanics
Double-inhomogeneity
Interacting Cracks and Ellipsoidal Inhomogeneities
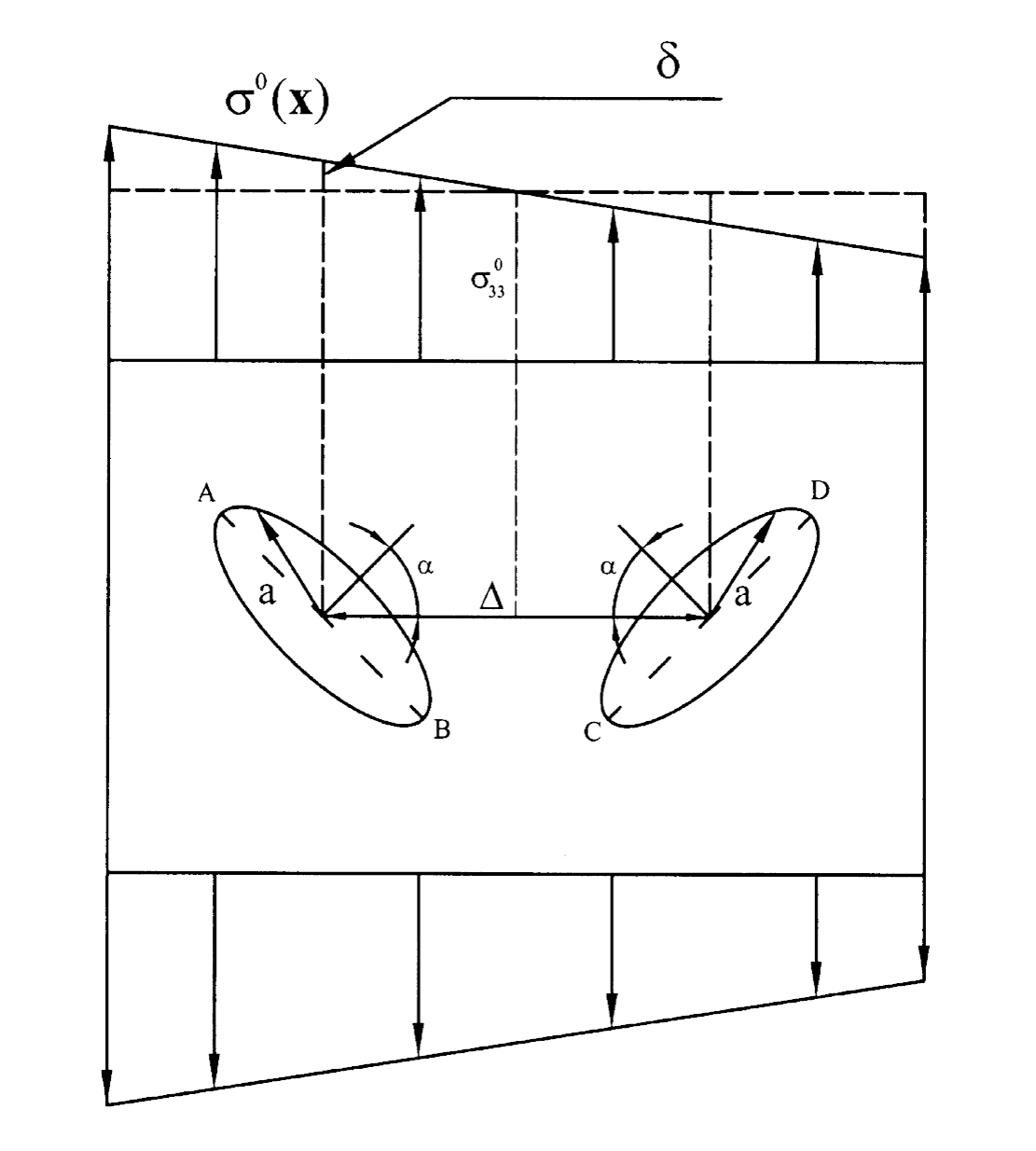
Penny shape cracks under linearly varying far-5eld applied stress.
Spectral Equivalent Inclusion Method
Tensor Spherical Harmonic Theories
Impotent Eigenstrain Fields
Novel Theories on MEE inclusions
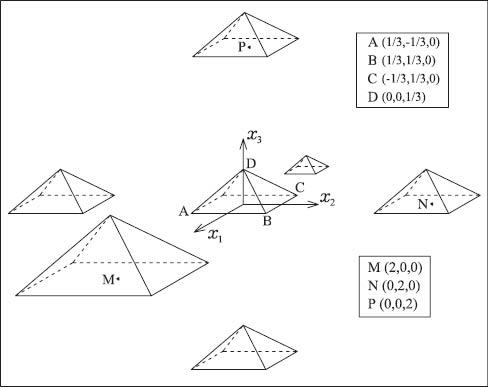
3D periodic distribution of pyramidal InN QDs within AlN barrier
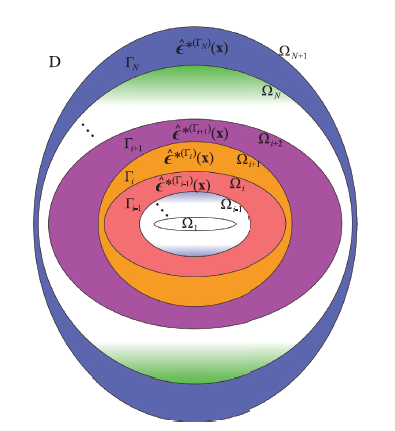
The generalized disturbance strains field
In this work, after formulating the weakly nonlocal micromorphic equations of motion for non-Bravais crystals with general anisotropy, specialization to diamond structures is made. A critical dilemma is the determination of the elastic moduli tensor appearing in the equations of motion. From the equivalency of these equations with the pertinent equations obtained in the context of lattice dynamics, the expressions of the components of the elastic moduli tensors in terms of the atomic force constants are derived analytically. Subsequently, the atomic force constants are calculated via ab initio density functional perturbation theory (DFPT) with high precision. As a benchmark for the accuracy and potency of the proposed theory, it is shown that the theory can capture not only all the acoustic branches but also all the optical branches of the dispersion curves for non-Bravais crystals like diamond and silicon over the entire first Brillouin zone. The accuracy of the results depends on the implemented order of the approximation of weakly nonlocal micromorphic theory. For illustration, the zeroth, tenth, and twentieth order approximations are employed to probe the dispersion curves pertinent to the crystallographic directions [100], [110], and [111] for diamond and silicon. For verification, the results are compared to those obtained independently from ab initio DFPT calculations.
By considering a single-walled carbon nanotube (SWCNT) as a two-dimensional elastica obtained from the roll-up of a graphene sheet into a circular tube, the present paper develops a precise well-posed continuum theory for describing the entire torsional behavior of SWCNTs from an initial unloaded state through their ultimate levels of loading. In addition, the proposed approach can capture the dual ideal shear strengths as well as the asymmetrical behavior of chiral tubes with respect to the direction of the applied torsional loading. The theory incorporates a highly nonlinear constitutive equation which provides information about the nanoscopic morphological parameters of the tubes. As it will be shown, the longitudinal and twist deformations are coupled. Accordingly, a parameter referred to as the torsion-induced extension will be defined.
In the literature, the analytical solutions concerned with the interaction between screw dislocation and surfaces/interfaces have been mainly limited to simple geometries and perfect interfaces. The focus of the current work is to provide an approach based on a rigorous semi-analytical theory suitable for treatment of such surfaces/interfaces that concurrently have complex geometry and imperfect bonding. The proposed approach captures the singularity of the elastic fields exactly. A vast variety of the pertinent interaction problems such as dislocation near a multi-inhomogeneity with arbitrary geometry bonded imperfectly to a matrix, dislocation near the free boundaries of a finite elastic medium of arbitrary geometry, and so on is considered. In the present approach the out-of-plane component of the displacement in each domain is decomposed as the displacement corresponding to a screw dislocation in a homogeneous elastic body of infinite extent and the disturbance displacement due to the interaction. Subsequently, the disturbance displacement in each medium is expressed in terms of eigenfunction expansion. Damaged interfaces are modeled by a spring layer of vanishing thickness, and the amount of damage is controlled via the stiffness of the spring. For the illustration of the robustness of the proposed methodology a variety of examples including the interaction of a screw dislocation with a circular as well as a star-shaped inhomogeneities, two interacting inhomogeneities, imperfectly bonded to an unbounded medium are given. Also, examples for highlighting the effect of free surfaces in the case of finite domains are provided. It is revealed that in the cases where matrix is stiffer than the inhomogeneity and the dislocation is inside the inhomogeneity, or the other way around, then the amount of interface damage can change the sign of the image force.
The multiphysics process of the electromagnetic (EM) radiation induced from an embedded nanofiber scatterer subjected to SH-waves is of interest. By discarding the commonly employed electroquasistatic approximation, the fully-coupled elastodynamics and Maxwell's equations have been solved simultaneously within the mathematical framework of piezoelectric surface elasticity theory. Certain subtleties regarding the introduced interface characteristic lengths that make the examination of the size effect on the EM radiated power, scattering cross section, fundamental resonance frequency, and distribution of the magnetic field possible will be discussed. The obtained results can be helpful for designing electrically small antennas, sensors, and resonators using piezoelectric nanofibers.
To account for certain essential features of material such as dispersive behaviour and optical branches in dispersion curves, a fundamental departure from classical elasticity to polar theories is required. Among the polar theories, micromorphic elasticity of appropriate grades and anisotropy is capable of capturing these physical phenomena completely. In the mathematical framework of micromorphic elasticity, in addition to the traditional elastic constants, some additional constants are introduced in the pertinent governing equations of motion. A precise evaluation of the numerical values of the aforementioned elastic constants in the realm of the experimentations poses serious difficulties. Thus this paper aims to provide a remedy as how to determine the micromorphic elastic constants theoretically in terms of the atomic force constants and lattice parameters of the crystalline solid with general anisotropy. In this treatment capture of the discrete nature of matter becomes an essential factor. To this end, the discrete lattice dynamics equations of a crystal are related to the pertinent anisotropic micromorphic equations of motion. This approach allows incorporating the symmetry groups of the crystals within lattice dynamics equations conveniently. For the illustration of the current theoretical developments, the micromorphic elastic constants of diamond and silicon crystals are computed in conjunction with ab initio density functional perturbation theory (DFPT). Moreover, the longitudinal and transverse optical and acoustic branches pertinent to [100] and [110] directions are presented. The accuracy of the results is verified by comparing the dispersion curves derived from the micromorphic theory, those of available experiments, and those directly obtained from DFPT calculations.
The phenomena of surface, interface, and size effects are the determinative factors in the prediction of the mechanical behavior of multiphase nanowires. The interatomic bond lengths and charge density distribution associated with the surface and interface layers of the relaxed configuration of such nanostructures, in the absence of any external loadings, differ from those of the bulk remarkably. Second strain gradient theory due to its competency in capturing the above mentioned effects will be employed to examine the relaxation of carbon-coated silicon nanowire, carbon nanoshell, and silicon nanowire. Using this theory their effective Young's modulus will also be estimated. To this end, the mathematical framework of second strain gradient theory will be presented in cylindrical coordinate system. For further illustrations, the Lamé type problem for a carbon nanotube where its inner and outer surfaces have strong, weak, and no interactions will be considered. Moreover, the size-dependent stress concentration phenomenon associated with an unbounded carbon plate weakened by a circular hole under remote biaxial loading is addressed. For verification of the theoretical treatment, the relaxation problems will be reexamined by employing atomistic simulation using LAMMPS and some suitable potentials.
The eccentricity between the circular fiber and its coating as well as the imperfection at the fiber-coating-matrix interfaces associated with certain composites can have a remarkable effect on the movement of a dislocation. For an in-depth understanding of such phenomena, the present work provides an exact analytical solution for the interaction between an eccentrically coated circular inhomogeneity embedded in an infinite elastic medium with imperfect interfaces and a screw dislocation. The dislocation may be located inside one of the regions: the core inhomogeneity, coating, or the matrix. The corresponding boundary value problem is solved by using conformal mapping and complex potential functions. The potential function associated with each region consists of a singular term which is the same as in the case where the dislocation is inside an infinite homogeneous medium made from the material of that region and some appropriate regular terms due to the presence of the two-phase inhomogeneity of interest. The regular parts of the solutions corresponding to the core inhomogeneity, coating, and the matrix are represented by Laurent series. In the general case of the eccentrically coated circular inhomogeneity and imperfect interfaces, the imposition of boundary conditions leads to some recursive relations which are very effective for the calculation of the unknown coefficients. For two special cases where: (1) the interfaces are perfect but eccentric, (2) the interfaces are imperfect but concentric, the exact closed-form expressions for the coefficients are obtained. For different ratios of the rigidities of the fiber and coating to the rigidity of the matrix, the effects of the amount of the eccentricity and imperfection at the interfaces on the variation of the image force in terms of the dislocation position are examined. Also the equilibrium positions and the corresponding stability status are discussed.
In this paper, Mindlin's second strain gradient theory is formulated and presented in an arbitrary orthogonal curvilinear coordinate system. Equilibrium equations, generalized stress-strain constitutive relations, components of the strain tensor and their first and second gradients, and the expressions for three different types of traction boundary conditions are derived in any orthogonal curvilinear coordinate system. Subsequently, for demonstration, Mindlin's second strain gradient theory is represented in the spherical coordinate system as a highly-practical coordinate system in nanomechanics. Second strain gradient elasticity have been developed mainly for its ability to capture the surface effects in the presence of micro-/nano- structures. As a numeric illustration of the theory, the surface relaxation of spherical domains in Mindlin's second strain gradient theory is considered and compared with that in the framework of Gurtin-Murdoch surface elasticity. It is observed that Mindlin's second strain gradient theory predicts much larger value for the radial displacement just near the surface in comparison to Gurtin-Murdoch surface elasticity.
The exact nature of the induced coupled-fields of anisotropic magneto-electro-elastic ellipsoidal inclusions, multi-inclusions, and inhomogeneities with non-uniform eigenfields under polynomial magneto-electro-elastic far-field loadings is of particular interest. For the sake of prediction of the induced coupled-fields of magneto-electro-elastic multi-inclusions due to piecewise polynomial generalized eigenfields several theorems and corollaries are stated and proved. Some classes of impotent generalized eigenfields associated with encapsulated ellipsoidal multi-inclusion result in vanishing generalized disturbance strains within the innermost ellipsoidal domain. On the other hand, it is found that there are certain classes of impotent generalized eigenfields for which the generalized disturbance stresses vanish everywhere. Furthermore, it is proved that there exists a unique equivalent magneto-electro-elastic inclusion associated with an anisotropic magneto-electro-elastic ellipsoidal inhomogeneity subjected to polynomial far-field loadings. It is shown that associated with every anisotropic magneto-electro-elastic ellipsoidal inhomogeneity, there exists a set of infinite numbers of far-field loadings for which the inhomogeneity does not induce any disturbance generalized stresses anywhere within the entire medium. In other words, under certain far-field loadings the inhomogeneity is not sensed by the surrounding magneto-electro-elastic medium.
It is well known that classical continuum theory has certain deficiencies in capturing the size effects and predicting the nanoscopic behavior of materials in the vicinity of nano-inhomogeneities and nano-defects with reasonable accuracy. Couple stress theory which is associated with an internal length scale for the medium is one of the higher order continuum theories capable of overcoming such difficulties. In this work, the problem of a nano-size fiber embedded in an unbounded isotropic elastic body for three different types of interface conditions: perfect, imperfect (partially damaged), and pure sliding (completely damaged) subjected to remote anti-plane loading is examined in this framework. The physically realistic size-dependent elastic fields for the problem will be derived analytically. The discontinuities of the displacement and rotation fields at the imperfect interfaces are assumed to be proportional to the associated reduced traction and couple traction, respectively. The effect of the interfacial damage on the stress field around the nano-fiber is also examined. Subsequently, the elastic field of a single nano-fiber with a damaged interface condition is employed in conjunction with the Mori-Tanaka theory to estimate the size-dependent overall anti-plane shear modulus of such solids enriched with unidirectional circular cylindrical fibers severely damaged at their interfaces with the matrix. The dependence of the anti-plane elastic shear modulus on several important physical parameters such as size, interface conditions, rigidity of the fiber, and the characteristic length of the constituents is analyzed. Finally, a variational approach for the estimation of the upper and lower bounds of anti-plane shear modulus will be given within couple stress elasticity and, moreover, the dependence of the bounds on the matrix-fiber interface damage and the fiber to the matrix rigidity ratio is examined.
In the present work, an analytical solution is presented for the scattering of transverse surface waves by a homogeneous piezoelectric fiber contained in a functionally graded piezoelectric half-space with exponential variation. The boundary value problem of interest is solved by constructing an appropriate set of multipole functions which satisfy: (a) the electromechanical field equations in the half-space, (b) the boundary conditions along its free surface, and (c) the far-filed radiation conditions. It is shown that the simple poles of these functions are related to the roots of the pertinent dispersion relation. For the case of electrically short condition along the free surface of the inhomogeneous half-space, the analytical expressions for the scattered electromechanical fields are derived. In the given numerical examples, the effects of such parameters as the frequency, the distance of the fiber to the substrate's free surface, and the coefficient in the exponent, indicating the variation of the electromechanical properties of the substrate on the scattered fields are addressed in detail. It is seen that these physical parameters have considerable effect on the dynamic response of the medium.
abstact
In this study, based on multipole expansion method an analytical treatment is presented for the anti-plane scattering of SH-waves by an arbitrarily oriented elliptic cavity/crack which is embedded near the interface between exponentially graded and homogeneous half-spaces. The cavity is embedded within the inhomogeneous half-space. The boundary value problem of interest is solved by constructing an appropriate set of multipole functions which satisfy (i) the governing equation in each half-space, (ii) the continuity conditions across the interface between the two half-spaces, and (iii) the far-field radiation and regularity conditions. The analytical expressions for the scattered elastodynamic fields are derived and the dynamic stress concentration factor associated with the elliptic cavity as well as the dynamic stress intensity factor relevant to the case of a crack are calculated. In the given numerical examples, the effects of such parameters as the incident wave number, angle of the incident waves, the distance of the cavity to the bimaterial interface, and the aspect ratio and the orientation of the elliptic cavity/crack on the scattered field are addressed in detail. It is seen that such parameters have significant effect on the dynamic response of the medium.
Capture of the discrete nature of crystalline solids for the purpose of the determination of their mechanical behavior with high precision is of interest. To achieve this objective, two fundamental contributing factors are on top of the list: (1) formulation in the mathematical framework of an appropriate higher order continuum theory rather than using classical treatment, and (2) incorporation of the true anisotropy of the media. The present work revisits Toupin-Mindlin first strain gradient theory for media with general anisotropy, and then specialize it to cubic crystals of hexoctahedral class. This formulation in addition to 3 classical material constants encountered in classical theory of elasticity, gives rise to 11 additional material parameters peculiar to first strain gradient theory. To date, there is no experimental method in the literature for the measurement of these parameters. A methodology incorporating lattice dynamics is proposed, by which all the material parameters including the classic ones are analytically expressed in terms of the atomic force constants. Subsequently, the analytical expressions for the nonzero components of the 4th and 6th order elastic moduli tensors as well as 6 characteristic lengths are derived. Finally, with the aid of ab initio calculations all the material properties in Toupin-Mindlin first strain gradient theory are numerically obtained with high precision. In this work the transformation matrices of cubic crystals of diploidal class which also falls under centrosymmetric point groups are discussed as well.
Accurate estimation of the in-plane shear modulus of solids reinforced by nano-/micro-size elliptical multi-coated fibers is the focus of this paper. It is well-known that at the scales comparable to the nanoscopic length scales of the material, traditional theory of elasticity ceases to hold and, moreover, due to lack of consideration of such length scales has an innate weakness of sensing the size effect. Therefore, it is proposed to formulate and calculate the effective shear modulus of the nano-/micro-composite within micropolar theory which introduces two material characteristic lengths into the field equations. For this purpose, Mori-Tanaka theory is extended to treat nested multi-inhomogeneity system in the mathematical framework of micropolar elasticity. The effective shear modulus pertinent to two cases of composites with aligned and randomly distributed enrichments is addressed. All the constituent phases are assumed to be micropolar media. As it will be seen, the estimations via couple stress and classical theories serve as the bounds of the estimate obtained using micropolar theory. The effects of the size and volume fraction of the fiber ensemble, the characteristic lengths and rigidity of the constituent phases, thickness of the coating layer, and the aspect ratio of the fiber ensemble on the effective shear modulus of the composite are examined.
The scattering of in-plane P- and SV-waves by a multi-coated circular nanofiber with deformable interfaces is of interest. To this end, in the present work, after introducing two kinds of interface momenta defined as the derivative of the interface excess kinetic energy with respect to the average and relative velocities at the interface, we extend the elastostatic theory of Gurtin et al. (1998) on deformable interfaces to the elastodynamic theory and derive the interface equations of motion using Hamilton principle. The effects of the generalized interface properties including the interface inertial parameters and interface stiffness towards stretch and slip on the dynamic stress concentration factor and the scattering cross section will be examined through some numerical examples. These results reveal that the effect of the interface inertial parameters becomes significant as the frequency of the incident wave increases. Moreover, as it will be shown, in the case where the interfaces are treated to be deformable, a larger number of resonance modes are captured for low-frequency waves as a result of the compliancy of the interfaces. It will also be seen that the resonant frequencies pertinent to the local deformations of the interface, increase with the interface stiffness parameters and decrease with the interface inertial parameters introduced in this work. These results can be used for tuning the resonant frequencies by selecting appropriate geometrical sizes and materials. Such phenomena can also be useful for designing locally resonant sonic materials with nano-sized lattice parameters.
Using the mathematical framework of surface elasticity theory, an analytical solution is presented for Love and Rayleigh surface wave propagations in a semi-infinite medium with face-centered cubic (fcc) single crystal structure. Previous formulations within surface elasticity have been based on the simplistic assumption of isotropy. Two different crystallographic orientations with respect to the incident wave vector are examined: (a) the free surface of the half-space is (010) plane and the surface waves propagate in [100] direction, (b) the free surface of the half-space is (110) plane and the surface waves propagate in direction. It is well-known that, contrary to the predictions based on classical theory, surface elasticity theory predicts Love waves can propagate in a homogeneous isotropic elastic fcc half-space and is dispersive. Moreover, Rayleigh wave propagation in a homogeneous single crystalline fcc half-space is dispersive. From the given numerical examples, it can be observed that Rayleigh wave propagation in Al half-space with (110) plane as its free surface is anomalous dispersive (AD), whereas in Ag, Au, Cu, Ni, and Pd half-space is normal dispersive (ND). On the other hand, Love wave propagation in Ag, Al, Au, Cu, Ni, and Pd half-spaces associated to either free surface layers, (010) and (110) is ND.
The present work aims to study the anti-plane scattering of SH-waves by an elastic micro-/nano-fiber which is embedded near the interface between exponentially graded and homogeneous half-spaces incorporating interface effects. The fiber is perfectly bonded to the inhomogeneous medium. It is well-known that traditional elasticity theory is incapable of accounting accurately for the nanoscopic-interfaces and, likewise, inappropriate for the prediction of the behavior of nano-sized structures where the surface-to-volume ratio is remarkably large. In the present study, the interface effects are incorporated using the well-known (Gurtin and Murdoch, 1975) surface elasticity theory which permits the use of continuum-based models to examine deformation at the nano-scale. Formulation in the mathematical framework of surface/interface elasticity gives rise to a set of non-classical boundary conditions across the interfaces. The boundary value problem of interest is solved by constructing an appropriate set of multipole functions which satisfy the governing differential equations in each half-space and the boundary conditions along the interface between the two half-spaces. The exact analytical expressions for the amplitude ratios of the reflected and transmitted waves are shown to depend on the elasticity parameters of the interface between the two half-spaces, in addition to the classical parameters of the bulk of these media. In the given numerical examples, the inevitable role of interfaces in the presence of nano-structure is well approved and it is shown that the interface effect is particularly remarkable for short wavelengths which are comparable to the interface characteristic lengths.
The present work aims to provide an accurate description of the tensile behavior of the planar as well as low-buckled stanene and to capture their ideal strength in armchair (AC)- and zigzag (ZZ)-directions. For an accurate description of anisotropic response of such hyperelastic materials as stanene, consideration of a highly nonlinear constitutive model in which up to the fourth power of strains is incorporated is inevitable. By utilizing first principles calculations based on density functional theory (DFT), the second, third, fourth, and fifth order elastic moduli tensors corresponding to both planar and low-buckled states are obtained. Moreover, the morphology of the free-standing stanene such as bond length and lattice parameter is determined; for low-buckled stanene two additional parameters, namely, buckling height and dihedral angle are computed. The effects of uniaxial and biaxial loadings germane to AC- and ZZ-directions on the buckling height and dihedral angle are also studied. Scrutinization of the electronic charge distribution reveals the phenomenon of the formation of necking in the Sn-Sn bonds under large uniaxial extension along the AC-direction. Moreover, the transformation of sp3 hybridized orbitals to sp2 hybridized orbitals is examined and confirmed through consideration of the structural geometries of the atomic bond angles.
Nowadays, by adding a small amount (about 0.5-5% by weight) of a desired nanomaterial to a matrix having certain properties one may design a multifunctional nanocomposites with a remarkably improved macroscopic properties of interest. The capability of conventional continuum theories in treating the problems of embedded ultra-small inhomogeneity with any of its dimensions comparable to the characteristic lengths of the involved constituent phases is questioned, mainly, on the grounds of the accuracy and the size effect. The micromechanical framework based on the Eshelby's ellipsoidal inclusion theory [1] which has been widely used to estimate the overall behavior of composites falls under the same category, as is size insensitive. In this work, effort is directed at the prediction of the macroscopic shear modulus of composites consisting of nano-/micro-size fibers of elliptic cross-sections via couple stress theory, a physically realistic theory that encompasses the size effect. To this end, the fundamental equations of couple stress elasticity in elliptic coordinates are derived and several fundamental elliptic inhomogeneity problems in plane couple stress elasticity are solved analytically. For the purpose of the application of these results to the study of the effective properties of the composites of interest, Mori and Tanaka theory [2] is first reformulated in the mathematical framework of couple stress theory. Subsequently, the overall shear modulus of solids reinforced by aligned as well as randomly oriented elliptic nanofibers will be predicted. The influences of the size, shape, orientation, rigidity, and intrinsic length of the reinforcing nanofibers as well as the effects of the characteristic length of the matrix on the effective shear modulus of the composite are addressed.
A smooth rigid circular anchor disk encapsulated by a penny-shaped crack is embedded in and unbounded transversely isotropic medium. The lamellar rigid disk exerts a nonuniform axisymmetric loading to the upper face of the crack. With the aid of an appropriate stress function and Hankel transform, the governing equations are converted to a set of triple integral equations which in turn are reduced to a Fredholm integral equation of the second kind. For some transversely isotropic materials the normalized stiffness of the system falls well outside of the envelope pertinent to isotropic media. It is shown that mode I stress intensity factor is independent of the material properties and solely depends on the ratio of the radius of the rigid disk to that of the crack; moreover, for the cases where this ratio is less than about 0.9 a simple explicit approximate expression for the mode I stress intensity factor is derived. In contrast, the normalized mode II stress intensity factor is independent of the mentioned geometrical parameters but depends on the elastic properties of the material; depending on the material properties, the normalized mode II stress intensity factor can vary between 0 to ∞ for transversely isotropic materials and between 0 to π/4 for isotropic materials.
Using the mathematical framework of surface/interface elasticity theory, an analytical solution is presented for the antiplane scattering of Love waves by a surface-breaking crack normal to the free surface of an ultra-thin layer bonded to a semi-infinite medium. Fourier transform technique is used to formulate the corresponding mixed-boundary value problem as a singular integral equation of Cauchy type. Within the context of the present theory, the scattered stress field, the Mode III dynamic stress intensity factor (DSIF) at the crack-tip, and the reflection coefficient at large distances from the crack face are computed and plotted for different wave numbers and surface/interface parameters. The dispersion relation is also derived within this framework. Contrary to the predictions based on classical theory, surface elasticity theory predicts that Love waves can propagate:(a) in an elastic half-space without the over-layer, and (b) in the layer-substrate system when the shear wave velocity of the layer is greater than that of the substrate. In the given numerical examples, the inevitable role of surfaces and interfaces in the presence of nano-structure is well approved and it is shown that the surface/interface effect is particularly remarkable for short wavelengths which are comparable to the surface/interface characteristic length.
Examination of the role of strain on the quantum spin hall (QSH) effect and band inversion for the monolayer of tin, stanene, is of interest. To this end, several uniaxial and biaxial strain loadings along the armchair (AC)- and zigzag (ZZ)-directions are applied using first principles calculations based on density functional theory (DFT). We observe QSH insulator as well as semi-metallic property associated with the strained stanene.
As long as the size of the embedded scatterer in comparison to the internal length scale of its surrounding elastic matrix is large, then the linear sampling method (LSM) and singular sources method (SSM) can be used in conjunction with classical theory of elasticity to reconstruct the size of the scatterer with reasonable accuracy. On the other hand, for the micro-/nano-size scatterer this treatment ceases to hold due to the shortcomings of classical theory of elasticity. Moreover, in the realm of this theory, wave propagation through a homogeneous medium is nondispersive on the macro-scale even for high frequency waves. This outcome is incompatible with the practical observations. A remedy to circumvent these shortcomings is to resort to such a higher order continuum theory as couple stress theory with micro inertia. In particular, by accounting for the micro inertia term a new length scale referred to as ”dynamic characteristic length” enters the equation of motion. Association of the media with positive or negative dispersion is a clear manifestation of the new formulation. Therefore, with attention to the aforementioned, both the direct and inverse scattering of high frequency SH-waves by a micro-/nano-size inhomogeneity embedded in an unbounded elastic isotropic medium are addressed in the mathematical framework of couple stress elasticity with micro inertia. It will be shown that for positive (negative) dispersion materials the couple stress phase velocity is greater (less) than the corresponding classical phase velocity. For the purpose of inverse scattering reconstruction of the micro-/nano-size scatterer the LSM and SSM are developed in the context of the proposed theory for the first time. It will be shown that LSM and SSM reconstructions of the size of the scatterer are unique.
For a better approximation of ring-shaped and toroidal cracks, a new eccentric annular crack model is proposed and an analytical approach for determination of the corresponding stress intensity factors is given. The crack is subjected to arbitrary mode I loading. A rigorous solution is provided by mapping the eccentric annular crack to a concentric annular crack. The analysis leads to two decoupled Fredholm integral equations of the second kind. For the sake of verification, the problem of a conventional annular crack is examined. Furthermore, for various crack configurations of an eccentric annular crack under uniform tension, the stress intensity factors pertaining to the inner and outer crack edges are delineated in dimensionless plots.
Propagation of shear horizontal surface acoustic waves (SHSAWs) within a functionally graded magneto-electro-elastic (FGMEE) half-space was previously presented (Shodja HM, Eskandari S, Eskandari M. J. Eng. Math. 2015, 1-18) In contrast, the current paper considers propagation of SHSAWs in a medium consisting of an FGMEE layer perfectly bonded to a homogeneous MEE substrate. When the FGMEE layer is described by some special inhomogeneity functions - all the MEE properties have the same variation in depth which may or may not be identical to that of the density - we obtain the exact closed-form solution for the MEE fields. Additionally, certain special inhomogeneity functions with monotonically decreasing bulk shear wave velocity in depth are considered, and the associated boundary value problem is solved using power series solution. This problem in the limit as the layer thickness goes to infinity collapses to an FGMEE half-space with decreasing bulk shear wave velocity in depth. It is shown that in such a medium SHSAW does not propagate. Using power series solution we can afford to consider some FGMEE layers of practical importance, where the composition of the MEE obeys a prescribed volume fraction variation. The dispersive behavior of SHSAWs in the presence of such layers is also examined.
The propagation of shear horizontal surface acoustic waves (SHSAWs) in an inhomogeneous magneto-electro-elastic (MEE) half-space with 6-mm symmetry is studied. By virtue of both the direct approach and Stroh-formalism, the dispersion relations corresponding to two general cases of material properties variation are obtained. In the first case, it is assumed that all material properties involving the MEE properties and density vary similarly in depth, whereas, the second case considers identical variation for the MEE properties, which differs from the variation of the density. The non-dispersive SHSAW velocities pertinent to the homogeneous MEE media are obtained under eight different surface electromagnetic boundary conditions as the limiting cases of the current study. The dispersion curves corresponding to eleven inhomogeneity profiles of practical importance are presented in an effective dimensionless format, and the effects of different types of inhomogeneity functions describing the composition of the functionally graded magneto-electro-elastic (FGMEE) half-space on the dispersion relation are discussed.
Nowadays, two-dimensional materials due to their vast engineering and biomedical applications have been the focus of many researches. The present paper proposes a large-deformation theory for thin plates with application to one-atom-thick layers (OATLs). The deformation is formulated exactly in the mathematical framework of Lagrangian description. In particular, an exact finite strain analysis is given - in addition to the usual strain tensor associated to the middle surface, the second and third fundamental forms of the middle surface of the deformed thin plate are also maintained in the analysis. Exact closed-form solutions for a uniaxially curved thin plate due to pure bending in one case and due to a combination of vertical and horizontal loading in another are obtained. As a special case of the latter problem, the exact solution for the plane-strain bulge test of thin plates is derived. Subsequently, the approximation of Vlassak and Nix [Vlassak, J.J., Nix, W.D., 1992. J. Mater. Res., 7(12), 3242-3249] for the load-deflection equation is recovered. The given numerical results are devoted to graphene as the most well-known OATL.
Surface/interface stresses, when notable, are closely associated with a surface/interface layer in which the interatomic bond lengths and charge density distribution differ remarkably from those of the bulk. The presence of such topographical defects as edges and corners amplifies the noted phenomena by large amounts. If the principal features of interest are such studies as the physics and mechanics of evolving microscopic-/nanoscopic-interfaces and the behavior of nano-sized structures which have a very large surface-to-volume ratio, traditional continuum theories cease to hold. It is for the treatment of such problems that augmented continuum approaches like second strain gradient and surface elasticity theories have been developed by Mindlin (1965) and Gurtin and Murdoch (1975), respectively. In the mathematical framework of the former theory, the surface effect is explicitly revealed through surface characteristic length and modulus of cohesion, whereas within the latter theory, which views the bulk material and its complementary surface as separate interacting entities, the critical role of surfaces/interfaces is directly incorporated through the introduction of the notions of tangential surface strain tensor, surface stress tensor, and surface elastic modulus tensor into the formulation. In the realm of the experimentations, evaluation of the above-mentioned surface parameters poses serious difficulties. One of the objectives of the current study is to provide a remedy as how to calculate, not only these parameters, but also Mindlin's bulk characteristic lengths as well as Lame constants with the aids of first principles density functional theory (DFT). To this end, surface elasticity is reformulated by maintaining the first and second gradients of the strain tensor for the bulk; as a result two new key equations are obtained. One of these equations is an expression for the net surface stress, needed to relate the surface parameters in surface elasticity to the Mindlin's second gradient theory parameters. The other equation is for the total elastic energy which is utilized to find an analytical expression for the surface energy. The available data on surface relaxation obtained experimentally and computationally are in good correspondence with the results of the current theory. Moreover, employing the present theory, an estimate for the effective elastic constants of films with infinite extension is provided.
Although, the evaluation of the nanohardness of amorphous silicon (a-Si) has been the subject of a few experimental works but, to date, it has not been addressed theoretically yet. In this work, first principles Kohn-Sham density functional theory (DFT)-based molecular dynamics (MD) in combination with Mohr-Coulomb criterion is employed to calculate the ideal shear strength of the damped MD annealed a-Si sample containing dangling and floating bonds which are pertinent to the threefold- and fivefold-coordinated defects, respectively, as well as distorted tetrahedral bonds. The stress state beneath the nanoindenter is triaxial, and is accounted for properly. The calculated values of nanohardness are in reasonable agreement with those values measured experimentally. Consideration of the electronic charge distribution under the state of triaxial tension test reveals that the yield phenomenon in a-Si is accompanied by the transformation of a threefold-coordinated Si atom to a fourfold-coordinated.
First principles density functional theory (DFT)-based molecular dynamics (MD) is used to study some physical and electronic properties of amorphous silicon (a-Si) samples, as-quenched and annealed containing dangling and floating bonds (pertinent to the threefold- and fivefold-coordinated defects, respectively) as well as distorted tetrahedral bonds. Surprisingly, except for the work of Pantelides (1986) who gave a rough estimate for the effective electron correlation energy, Ueff of a floating bond on the fivefold-coordinated Si, to date, there are no theoretical studies in the literature for the calculation of Ueff pertinent to this type of defect. In this work, Ueff for each type of defect, namely, threefold- and fivefold-coordinated atoms which are present in our generated annealed a-Si sample at 300 K is calculated by the current ab initio framework. We found that, Ueff for the fivefold-coordinated Si varies from +0.32 to +0.41 eV, whereas for the threefold-coordinated Si it ranges between -0.33 to +0.04. The electronic, optoelectronic, and transport properties of a-Si semiconductors are directly influenced by gap tuning which in turn is controlled by the applied strains. The effects of temperature and strain on the mobility gap and the electronic density of states (DOS) for the a-Si samples are of particular interest. For the unstrained as-quenched and annealed samples at T = 0 K, the mobility gap is calculated to be equal to 1.42 and 1.47 eV, respectively; whereas, at T = 300 K these values change to 1.17 and 1.24 eV, respectively. At T = 0 K, for both samples under the uniaxial tensile strains below 0.070, the calculated mobility gap is about 1.4 eV which sharply decreases by applying strain beyond 0.070. As it will be seen, the gap regions for both the unstrained sample and the strained sample with ϵ33 = 0.070 contain midgap states, but for the strained samples with the higher strains of ϵ33 = 0.140 and 0.210 the midgap states disappear.
The critical condition for the generation of a screw misfit dislocation dipole (MDD) at the interface between a nanowire (NW) with uniform shear misfit strain and its surrounding unbounded matrix within surface/interface elasticity theory is of particular interest. The analysis is carried out using the complex potential variable method. It is shown that the critical radius of the NW corresponding to the onset of the MDD generation decreases with the increase in the uniform shear eigenstrain inside the NW as well as when the stiffness of the NW increases with respect to the matrix. The critical radius strongly depends on the non-classical interface parameter. Comparison is made with classical solution, which can be obtained as the special case of the surface/interface elasticity theory.
The inadequacy of traditional theory of elasticity in describing such a phenomenon as dispersion associated to a propagating wave with wavelength comparable to the intrinsic length of the medium of interest is well-known. Moreover, under certain circumstances it is incapable of capturing all the propagating waves. A remedy to such dilemmas is the employment of the more accurate higher order continuum theories which give rise to the appearance of at least one new characteristic length in the formulation. The experimental evidences as well as lattice dynamic analysis suggest that, although higher order continuum theories result in some improvements, but cannot fully overcome the above-mentioned dilemmas, unless the micro inertia term is included in the formulations. The current work addresses the elastodynamic fields of an anti-plane shear wave scattered by a micro-/nano-fiber embedded in an infinite matrix using couple stress theory with micro inertia term. Moreover, the formulations pertinent to the cases where the incident wave strikes an embedded micro-/nano-size circular cavity or a rigid immovable micro-/nano-fiber are also obtained. Within this theory, the appearance of a new length scale, so-called “dynamic characteristic length” stems from consideration of the micro inertia, which gives rise to physically realistic dispersion relations with characteristic resembling those observed in experiments. The effects of two different types of boundary conditions for the cases of elastic and rigid immovable fiber encountered within the present theory are discussed. By using this theory, the corresponding analytical expressions of the elastodynamic fields, total and differential scattering cross-sections, and the dynamic stress concentration factor are presented and their dependence on the characteristic lengths and frequency are examined. It has been shown that the effect of micro inertia term is more noticeable in higher frequencies.
Free vibration of laminated micro-plates with arbitrary geometry and boundary conditions consisting of several micro-layers with free sliding/frictional sliding/perfect interfaces is of interest. The inter-layer bond in the direction normal to the interfaces is perfect, and thus the corresponding displacement component is continuous across the interfaces. The mentioned in-plane interface conditions may be realized by varying the stiffness of the sliding inter-layer spring of vanishing thickness. For free sliding and perfect interface conditions the stiffness→0 and , respectively. Couple stress theory as a useful higher order continuum theory is utilized to formulate the problem. Subsequently, the corresponding Hamiltonian is presented. The three components of the displacement field in each layer are given by three distinct expressions; each expression consists of the product of a base function and three dimensional polynomials with unknown coefficients. The base functions are chosen according to the geometries of the system and the corresponding layer and to satisfy the homogeneous essential boundary conditions. For the enforcement of the displacement continuity in the direction normal to the interfaces, an appropriate series with unknown coefficients pertinent to each layer is added. The influences of the level of inter-layer imperfection and couple stress on the dynamical characteristics including the angular frequencies of free vibration and the corresponding mode shapes are addressed.
Carbon nanotubes (CNTs) with and without end caps may be used for fluid storage and transport, respectively, referred to as CNT-nanovessel and CNT-nanopipe. The determination of the stiffness in the hoop (circumferential) and radial directions, ideal hoop strength, and hoop stress-strain curve of such nanostructures is of particular interest. Due to the proposed viewpoint, a chiral free-standing single-walled CNT (SWCNT) has a natural angle of twist and natural extension along the axis of the tube. For example, for the SWCNT (9,3) with diameter of 0.85 nm and chirality angle of 13.9°, the natural angle of twist per unit length is rad/nm. Previously, only Vercosa et al. (2010) who used extended tight-binding calculations have noticed the natural twist. The work of Delfani et al. (2013) and the current study are the first to lay down an analytical formulation for arriving at this phenomenon. This natural angle of twist has a remarkable effect on both the mechanical and electronic properties of chiral CNTs. It will be shown that application of the internal pressure results in twist of the chiral CNT-nanovessels/nanopipes. The sign change in the angle of twist associated with a tube of a given structural index occurs at a certain level of internal pressure (hoop strain), which progressively increases with the tube's radius. In the present work, the description of the mentioned properties is achieved through an exact analytical formulation in the framework of continuum mechanics for large deformations. To this end, a strain energy density function which includes the chirality angle of the CNT as well as the fourth-, sixth-, eighth-, and tenth-order elastic moduli tensors of graphene is proposed. In the context of the current study, SWCNT is an elastica obtained from bending of a graphene sheet, and the graphene sheet may be referred to as a lamina. Accounting for the residual elastic fields, commonly neglected by other authors, within a free-standing CNT, merely resulted from bending of graphene, is indeed essential for an accurate analysis of the CNT subjected to subsequent internal pressure. A key feature of the present formulation lies in its simplicity without resort to approximations, empirical potentials, or costly ab initio calculations. Availability of analytical solution provides an in-depth insight to the mechanical behavior of CNTs. In particular, among the analytical expressions, the exact closed-forms for the radial and hoop Young's moduli and hoop ideal strength for CNT-nanovessels/nanopipes are derived.
It is well-known that classical continuum theory has certain deficiencies in predicting the nanoscopic behavior of materials in the vicinity of defects. Couple stress theory is one of the higher order continuum theories which can overcome such difficulties by introducing new characteristic length. An accurate analytical determination of the elastic fields of an embedded circular nano/micro-rigid fiber with damaged interface under remote anti-plane loading in the context of couple stress elasticity is of particular interest.
In this paper an analytical approach to study the effect of the substrate physical properties on the kinetics of adhesion and motility behavior of cells is presented. Cell adhesion is mediated by the binding of cell wall receptors and substrate's complementary ligands, and tight adhesion is accomplished by the recruitment of the cell wall binders to the adhesion zone. The binders' movement is modeled as their axisymmetric diffusion in the fluid-like cell membrane. In order to preserve the thermodynamic consistency, the energy balance for the cell-substrate interaction is imposed on the diffusion equation. Solving the axisymmetric diffusion-energy balance coupled equations, it turns out that the physical properties of the substrate (substrate's ligand spacing and stiffness) have considerable effects on the cell adhesion and motility kinetics. For a rigid substrate with uniform distribution of immobile ligands, the maximum ligand spacing which does not interrupt adhesion growth is found to be about 57 nm. It is also found that as a consequence of the reduction in the energy dissipation in the isolated adhesion system, cell adhesion is facilitated by increasing substrate's stiffness. Moreover, the directional movement of cells on a substrate with gradients in mechanical compliance is explored with an extension of the adhesion formulation. It is shown that cells tend to move from soft to stiff regions of the substrate, but their movement is decelerated as the stiffness of the substrate increases. These findings based on the proposed theoretical model are in excellent agreement with the previous experimental observations.
First principles Kohn-Sham density functional theory (DFT)-based molecular dynamics (MD) is employed to investigate some physical and mechanical properties of amorphous Si (a-Si) samples, as-quenched and annealed containing dangling and floating bonds as well as distorted tetrahedral bonds. The total energy and true stress as functions of the engineering strain for a-Si samples subjected to uniaxial tensile stress as well as uniaxial extension are obtained. It is well-known that the electron density of the state of matters can be determined via ab initio DFT-based MD with high accuracy. Using this technique, such inherent properties as the elastic constants, ideal tensile strength, ultimate tensile strength, and surface and cohesive energies will be calculated. Since the employed ab initio MD, in contrast to the empirical potentials simulations, is capable of providing the evolution of the electronic charge distribution, we can afford to study the chemistry of crack initiation and reconstructed surfaces at final rupture. The calculated cohesive and surface energies are compared with the available theoretical and experimental results; Tyson's empirical relation and universal binding energy relations (UBERs) are also examined. The calculated elastic constants using the symmetry-general scheme satisfy well the isotropic relation. To date, the ab initio MD samples of a-Si generated from the completely melted scheme were all free of three-fold-coordinated Si. In contrast, as we will show, by implementing special thermal treatments, generation of all inherent structural defects is possible. Based on the electronic charge distribution, dative bonds and trigonal prisms for, respectively, floating and dangling bonds have been observed.
The dynamic equivalent inclusion method (DEIM) which was first proposed by Fu and Mura (1983), in its original context has some shortcomings, which were pointed out and remedied by Shodja and Delfani (2009) who introduced the new consistency conditions along with the related micromechanically substantiated notion of eigenstress and eigenbody-force fields. However, these theories are bound to elastic media with isotropic phases. The present work extends the idea of the above-mentioned new DEIM to the dynamic electro-mechanical equivalent inclusion method (DEMEIM) for the treatment of the scattering of SH-waves by a two-phase circular piezoelectric obstacle bonded to a third phase piezoelectric matrix. All the three transversely isotropic media have the same rotational axis of symmetry and the same poling direction which are parallel to the axis of the coated fiber, but perpendicular to the direction of propagation of the incident SH-wave. In general, the nested circular media are considered to be eccentric, i.e., the core fiber has a coating with variable thickness. Realization of the nature of the behavior of the field quantities a priori and its appropriate implementation in to the new extended consistency conditions is a critical step to insure a rigorous mathematical framework. As it will be shown, the expansion of the Green's function and the eigenelectric, eigenstress, and eigenbody-force fields in terms of the eigenfunctions of the pertinent field equations rather than the commonly considered polynomials in the traditional equivalent inclusion method (EIM) leads to an accurate solution with high convergence rate. The exact analytical expression for the total scattering cross-section which is influenced by the piezoelectric couplings is derived. The effects of the piezoelectric couplings and the properties of the fiber, coating, and the matrix as well as the wave number on the electro-mechanical scattered fields are examined.
The so-called enriched weight functions (EWFs) are utilized in mesh-free methods (MMs) to solve linear elastic fracture mechanics (LEFM) problems; the following issues are of concern: convergence behavior; sufficiency of EWFs to capture singular fields around the crack-tip; and the preservation of the J-integral path-independency. EWFs prove useful in conjunction with the moving least square reproducing kernel method (MLSRKM); for this purpose, both EWFs and MLSRKM are modified. Since EWFs are not truly representative of the near-tip solution, fully EWFs (FEWFs) are introduced. Finally, some descriptive examples address the aforementioned concerns and the accuracy and efficacy of the proposed technique.
An accurate determination of the two- and three-dimensional electro-elastic fields of periodically as well as arbitrarily distributed interacting quantum wires (QWRs) and interacting quantum dots (QDs) of arbitrary shapes within a piezoelectric matrix is of particular interest. Both the QWR/QD and the barrier may be made of materials with distinct general rectilinear anisotropy in elastic, piezoelectric, and dielectric constants. The lattice mismatch between the QWR/QD and the barrier is accounted by prescribing an initial misfit strain field within the QWR/QD. Previous analytical treatments have neglected the distinction between the electro-mechanical properties of the QWR/QD and those of the barrier. This simplifying assumption is circumvented in the present work by using a novel electro-mechanical equivalent inclusion method in Fourier space (FEMEIM). Moreover, the theory can readily treat cases where the QWRs/QDs are multiphase or functionally graded (FG). It was proven that for two-dimensional problems of either a periodic or an arbitrary distribution of FG QWRs in a transversely isotropic piezoelectric barrier, the elastic and electric fields are electrically and elastically impotent, respectively, and no electric field would be induced in the medium provided that the rotational symmetry and polarization axes coincide. Some numerical examples of more frequent shapes and different distributions of indium nitride QDs/QWRs within transversely isotropic aluminum nitride barrier are solved.
In this work, a general semi-analytical method for the determination of the elastic fields within an anisotropic homogeneous elastic solid with an inclined edge or interior crack is developed. In this method, the displacement field is represented as a sum of a function and a finite series of functions with unknown coefficients. The functions are constructed in such a way that all the essential homogeneous and inhomogeneous boundary conditions are satisfied exactly and, moreover, the displacement discontinuity across the crack faces as well as the exact singular behaviour of the stress field at the crack-tip are captured. The unknown coefficients are determined by utilizing the principle of minimum potential energy; the obtained coefficients matrix involves some singular integrands which for their accurate integrations over the domain in the vicinity of the crack-tip the generalized Duffy transformation is employed. Following the calculations of the unknown coefficients, the displacement field and subsequently the remaining field quantities are obtained. The fracture parameters, stress intensity factor SIF and the crack opening displacement COD are readily evaluated. Comparisons of the solutions of several examples obtained by the current approach with the exact solutions reveal the efficacy of the proposed method.
The normal indentation of a rigid circular disk into the surface of a transversely isotropic half-space reinforced by a buried inextensible thin film is addressed. By virtue of a displacement potential function and the Hankel transform, the governing equations of this axisymmetric mixed boundary value problem are represented as a dual integral equation, which is subsequently reduced to a Fredholm integral equation of the second kind. Two important results of the contact stress distribution beneath the disk region as well as the equivalent stiffness of the system are expressed in terms of the solution of the Fredholm integral equation. When the membrane is located on the surface or at the remote boundary, exact closed-form solutions are presented. For the limiting case of an isotropic half-space the results are verified with those available in the literature. As a special case, the elastic fields of a reinforced transversely isotropic half-space under the action of surface axisymmetric patch loads are also given. The effects of anisotropy, embedment depth of the membrane, and material incompressibility on both the contact stress and the normal stiffness factor are depicted in some plots.
The misfit strain within the core of a two-phase free-standing core-shell nanowire resulting in the generation of an edge misfit dislocation or an edge misfit dislocation dipole at the core-shell interface is considered theoretically within both the classical and surface/interface elasticity approaches. The critical conditions for the misfit dislocation generation are studied and discussed in detail with special attention to the non-classical surface/interface effect. It is shown that this effect is significant for fine cores of radius smaller than roughly 20 interatomic distances. The positive and negative surface/interface Lamé constants mostly make the generation of the misfit dislocation easier and harder, respectively. Moreover, the positive (negative) residual surface/interface tensions mostly make the generation of the misfit dislocation harder (easier). The formation of individual misfit dislocation is energetically more preferential in finer two-phase nanowires, while the formation of misfit dislocation dipole is more expectable in the coarser ones.
The elastic behaviors of a two-axes dipole of wedge disclinations and an individual wedge disclination located inside the shell of a free standing core-shell nanowire is studied within the surface/interface elasticity theory. The corresponding boundary value problem is solved using complex potential functions, defined through modeling the disclination dipole by two finite walls of infinitesimal edge dislocations. The stress field, disclination strain energies and image forces acting on the disclinations, are calculated and studied in detail. It is shown that the stresses are rather inhomogeneous across the nanowire cross section, change their signs and reach local maxima and minima far from the disclination lines in the bulk or on the surface of the nanowire. For negative values of the surface/interface modulus and relatively small values of the ratio of the shell and core shear moduli, the surface/interface effect manifests itself through non-classical stress oscillations along the shell free surface in the case of a disclination dipole and core-shell interface in both the cases of a disclination dipole and an individual disclination. The non-classical solution for the strain energy deviates from the classical solution with different effects caused by the surface/interface moduli on the wedge disclination dipole and an individual disclination. When the core is softer than the shell, the dipole with radial orientation of its arm has an unstable equilibrium position in the shell. In general, if the surface/interface modulus is positive, the surface/interface effects are rather weak; however, if it is negative, the effect can be very strong, especially near the shell surface. Previous article in issue
Certain physical and mechanical phenomena within ultra-thin face-centered cubic (fcc) films containing common types of interacting point defects are addressed. An atomic-scale lattice statics in conjunction with many-body interatomic potentials suitable for binary systems is conducted to analyze the effects of the depth on the: (1) formation energy and layer-by-layer displacements due to the presence of vacancy-octahedral self-interstitial atom (OSIA) ensemble, and (2) elastic fields as well as the free surface shape in the case of vacancy-dopant interaction. Moreover, the effects of the inter-defect spacing for various depths are also examined. To ensure reasonable accuracy and numerical convergence, the atomic interaction up to the second-nearest neighbor is considered.
The elastic behavior of an arbitrary oriented wedge disclination dipole located inside a nanowire, which in turn is embedded in an infinite matrix, is studied within the surface/interface theory of elasticity. The corresponding boundary value problem is provided using complex potential functions. The potential functions are defined through modeling the wedge disclination in terms of an equivalent distribution of edge dislocations. The interface effects on the stress field and strain energy of the disclination dipole and image forces acting on it, the influence of relative shear moduli of the nanowire and the matrix, as well as the different characteristics of the interface are studied thoroughly. It is shown that the positive interface modulus leads to increased strain energy and extra repulsive forces on the disclination dipole. The noticeable effect of the negative interface modulus is the non-classical oscillations in the stress field of the disclination dipole and an extra attractive image force on it.
Mindlin's (1965) second strain gradient theory due to its competency in capturing the effects of edges, corners, and surfaces is of particular interest. Formulation in this framework, in addition to the usual Lame constants, requires the knowledge of sixteen additional materials constants. To date, there are no successful experimental techniques for measuring these material parameters which reflect the discrete nature of matter. The present work gives an accurate remedy for the atomistic calculations of these parameters by utilizing the first principles density functional theory (DFT) for the calculations of the atomic force constants combined with an analytical formulation. It will be shown that writing the consistency conditions obtained from the equivalency between the atomistic crystal lattice dynamics of the bulk material and its counterpart in the second strain gradient elasticity is insufficient for the calculations of all the additional constants. As it will be discussed, there are two missing conditions which are then provided by consideration of the free standing film problem that bring the surface effect into account. As a consequence of surface effect consideration, the modulus of cohesion which is one of the important additional constants is calculated. Moreover, an analytical expression for the surface energy in terms of the modulus of cohesion, Lame constants, materials characteristic lengths, and the film thickness is presented. If the film thickness is much bigger than the magnitude of the characteristic lengths of the material, then the surface energy would no longer depend on the film thickness.
The elastic behavior of an edge dislocation placed in the shell of a free-standing core-shell nanowire is considered within the theory of surface/interface elasticity. Using the method of complex potential functions the expressions for the stress field of the dislocation, image forces on the dislocation, and the dislocation strain energy are derived and studied in detail. A special attention is paid to non-classical effects revealed within the surface/interface elasticity approach where a characteristic length parameter referred to as surface/interface modulus is introduced. These effects are (i) the stress oscillations along the shell surface and core-shell interface for negative values of the surface/interface elastic moduli; (ii) a strong dependence of image forces on the core size; (iii) extra repelling (attraction) of the dislocation from (to) the shell surface and core-shell interface characterized by positive (negative) interface modulus; and (iv) a decrease of the dislocation strain energy in the central region of the shell and its local increase with an extra maximum in the vicinity of the shell surface for negative values of the surface/interface elastic moduli. These non-classical effects increase with diminishing core radius and shell thickness and are very strong in the layers of 1 nm thickness adjacent to the core-shell interface and shell surface. The effects of the residual surface stress are also addressed.
By utilizing the fourth-, sixth-, eighth-, and tenth-order elastic moduli tensors of graphene a highly nonlinear constitutive model for it is proposed. Subsequently, an accurate analytical formulation, describing the entire tensile behavior of single-walled carbon nanotubes (SWCNTs) from their initial unloaded states through their ideal strengths, is made possible. The angle of twist which is a critical parameter that varies with the tensile loading is also calculated within the current framework. The estimated value of the theoretical strength of SWCNTs with different chiralities and radii as well as that of graphene ranges from 0.39 to 0.44 TPa. Some peculiarities associated with chirality of 15° are observed.
Incorporation of the first gradient of strain, in addition to the strain itself, into the strain energy density of an elastic solid leads to Mindlin's first strain gradient theory, which is useful for examination of size effect as well as other mechanical phenomena at the nano-scale. For isotropic elastic solids, the first strain gradient theory, in addition to the two independent Lamé constants, gives rise to five new material constants which in turn reduce to two material parameters, and with dimension of length. The evaluation of these parameters, however, has posed serious challenges, both experimentally and theoretically. In this work ab initio method is used to compute the characteristic lengths for several fcc and bcc metal crystals. It will be seen that the elements of the Hessian matrix, obtained by taking the second derivatives of the total energy with respect to the atomic positions, are linked to the strain gradient material constants.
The elastica is referred to the shape of the curve into which the centreline of a flexible lamina is bent. Hence, single-walled carbon nanotubes (SWCNTs) are treated as the elastica obtained from bending of graphene. The corresponding large deformation accompanies both the material and geometrical non-linearities. The morphology of the free-standing SWCNTs such as the natural angle of twist, bond lengths, tube radius and wall thickness are determined. Moreover, it is shown that the induced self-equilibriated strain field has a remarkable impact on the mechanical behaviour of the nanotube. Utilization of an appropriate non-linear continuum constitutive relation for graphene leads to exact formulation of the governing equations of SWCNTs. Subsequently, through perturbation analysis, the asymptotic solutions of the initial elastic fields for the SWCNTs are presented. By performing ab initio calculations, the components of the fourth and sixth-order elastic moduli tensors in the constitutive model of graphene needed in this study are computed.
The asymmetric problem of lateral translation of an inextensible circular membrane embedded in a transversely isotropic half-space is addressed. With the aid of appropriate Green's functions, the governing equations of the problem are written as a set of coupled integral equations. With further mathematical transformations, the system of dual integral equations is reduced to two coupled Fredholm integral equations of the second kind which are amenable to numerical treatments. The exact closed-form solutions corresponding to two limiting cases of a membrane resting on the surface of a half-space and embedded in a full-space are derived. The jump behavior of results at the edge of the membrane for the case of an infinitesimal embedment is highlighted analytically. For the special case of an isotropic half-space, the results are in exact agreement with those available in the literature. The detailed numerical scheme for solving the coupled Fredholm integral equations is presented. Selected numerical results are depicted and the effects of anisotropy on the lateral stiffness factor are discussed.
The determination of the interstitial sites and saddle points corresponding to the diffusion of an interstitial atom in ultrathin face-centered cubic (fcc) film is of particular interest. The outcome is strongly influenced not only by the orientation of the free surface but also by the location of the defect with respect to the free surface and film-rigid substrate interface. In this article, an atomic-scale simulation is conducted to analyze the effects of depth on the out-of-plane interstitial mechanism of diffusion. To ensure reasonable accuracy and numerical convergence, the atomic interaction up to the second-nearest neighbor is considered. The ab initio examination of the above-mentioned problem associated with thin films requires a large supercell and is computationally time consuming. However, for the sake of demonstration, the values of the barrier height energy pertinent to a diffusing self-interstitial atom in the bulk material are computed using both the first principles density functional theory (DFT) and the developed technique, indicating reasonable correspondence.
An analytical approach which is popular in micromechanical studies has been extended to the solution for the interference fit problem of the femoral stem in cementless total hip arthroplasty (THA). The multiple inhomogeneity problem of THA in transverse plane, including an elliptical stem, a cortical wall, and a cancellous layer interface, was formulated using the equivalent inclusion method (EIM) to obtain the induced interference elastic fields. Results indicated a maximum interference fit of about 210 μm before bone fracture, predicted based on the Drucker-Prager criterion for a partially reamed section. The cancellous layer had a significant effect on reducing the hoop stresses in the cortical wall; the maximum press fit increased to as high as 480 μm for a 2 mm thick cancellous. The increase of the thickness and the mechanical quality, i.e., stiffness and strength, of the cortical wall also increased the maximum interference fit before fracture significantly. No considerable effect was found for the implant material on the maximum allowable interference fit. It was concluded that while larger interference fits could be adapted for younger patients, care must be taken when dealing with the elderly and those suffering from osteoporosis. A conservative reaming procedure is beneficial for such patients; however, in order to ensure sufficient primary stability without risking bone fracture, a preoperative analysis might be necessary.
Eshelby's theories on the nature of the disturbance strains due to polynomial eigenstrains inside an isotropic ellipsoidal inclusion, and the form of homogenizing eigenstrains corresponding to remote polynomial loadings in the equivalent inclusion method (EIM) are not valid for spherically anisotropic inclusions and inhomogeneities. Materials with spherically anisotropic behavior are frequently encountered in nature, for example, some graphite particles or polyethylene spherulites. Moreover, multi-inclusions/inhomogeneities/inhomogeneous inclusions have abundant engineering and scientific applications and their exact theoretical treatment would be of great value. The present work is devoted to the development of a mathematical framework for the exact treatment of a spherical multi-inhomogeneous inclusion with spherically anisotropic constituents embedded in an unbounded isotropic matrix. The formulations herein are based on tensor spherical harmonics having orthogonality and completeness properties. For polynomial eigenstrain field and remote applied loading, several theorems on the exact closed-form expressions of the elastic fields associated with the matrix and all the phases of the inhomogeneous inclusion are stated and proved. Several classes of impotent eigenstrain fields associated to a generally anisotropic inclusion as well as isotropic and spherically anisotropic multi-inclusions are also introduced. The presented theories are useful for obtaining highly accurate solutions of desired accuracy when the constituent phases of the multi-inhomogeneous inclusion are made of functionally graded materials (FGMs).
The elastic behavior of an edge dislocation located inside the core of a core-shell nanowire which is embedded in an infinite matrix is studied within the surface/interface elasticity theory. The corresponding boundary value problem is solved exactly by using complex potential functions. An important parameter so-called interface characteristic parameter which has the dimension of length and is a combination of the interface moduli enters the formulations. The stress field of the dislocation, image force acting on the dislocation, and the dislocation strain energy is calculated by considering the interface effect. The introduced characteristic parameter allows the examination of the core-shell size on the image forces acting on the dislocation. The repelling and attracting effects of the interface parameter on the image force are discussed. The equilibrium position of the dislocation is also studied. The dislocation strain energy in the interface elasticity framework is only slightly different from that of traditional elasticity when the dislocation is placed in the central region of the core and reaches its maximum value when it is located near the core-shell interface.
Consider a set of (N+1)-phase concentric spherical ensemble consisting of a core region encased by a sequence of nested spherical layers. Each phase is spherically isotropic and is functionally graded (FG) in the radial direction. Determination of the elastic fields when the outermost spherical surface is subjected to a nonuniform loading and the constituent phases are subjected to some prescribed nonuniform body force and eigenstrain fields is of interest. When the outermost layer is an unbounded medium with zero eigenstrain and body force fields, then an N-phase multi-inhomogeneous inclusion problem is realized. Based on higher-order spherical harmonics, presenting a three-dimensional strain formulation with a robust form of compatibility equations, a spectral theory of elasticity in the spherical coordinate system is developed. Application of the established spectral theory leads to the exact closed-form solution when the elastic moduli of each phase vary as power-law functions of radius.
The elastic behavior of a screw dislocation which is positioned inside the shell domain of an eccentric core-shell nanowire is addressed with taking into account the surface/interface stress effect. The complex potential function method in combination with the conformal mapping function is applied to solve the governing non-classical equations. The dislocation stress field and the image force acting on the dislocation are studied in detail and compared with those obtained within the classical theory of elasticity. It is shown that near the free outer surface and the inner core-shell interface, the non-classical solution for the stress field considerably differs from the classical one, while this difference practically vanishes in the bulk regions of the nanowire. It is also demonstrated that the surface with positive (negative) shear modulus applies an extra non-classical repelling (attracting) image force to the dislocation, which can change the nature of the equilibrium positions depending on the system parameters. At the same time, the non-classical solution fails when the dislocation approaches very close to the surface/interface with negative shear modulus. The effects of the core-shell eccentricity and nanowire diameter on dislocation behavior are discussed. It is shown that the non-classical surface/interface effect has a short-range character and becomes more pronounced when the nanowire diameter is smaller than 20 nm.
In this paper, the scattering of anti-plane shear waves in an infinite matrix containing a multi-coated nanofiber/nanotube is studied. Based on the fact that the surface to volume ratio for nano-size objects increases, the usual classical theories which generally neglect the surface/interface effects fail to provide reasonable results. Therefore, to analyze the problem the wave-function expansion method is coupled with the surface/interface elasticity theory. In order to provide some quantitative results through consideration of several examples, the knowledge of the relevant surface and/or interface properties of the corresponding constituent materials are required. For this reason, part of this work is devoted to the development of the method of calculation of these properties. Subsequently, the surface shear modulus and residual stresses of several fcc materials as well as interface shear modulus and residual stresses of some fcc-fcc bicrystals are computed. For determination of these parameters a molecular dynamics program which uses Rafii-Tabar and Sutton interatomic potential function is addressed. In numerical calculations, the essential role of surfaces and interfaces in nano-scale is well approved.
In addition to enhancement of the results near the point of application of a concentrated load in the vicinity of nano-size defects, capturing surface effects in small structures, in the framework of second strain gradient elasticity is of particular interest. In this framework, sixteen additional material constants are revealed, incorporating the role of atomic structures of the elastic solid. In this work, the analytical formulations of these constants corresponding to fee metals are given in terms of the parameters of Sutton-Chen interatomic potential function. The constants for ten fcc metals are computed and tabulized. Moreover, the exact closed-form solution of the bending of a nano-size Bernoulli-Euler beam in second strain gradient elasticity is provided; the appearance of the additional constants in the corresponding formulations, through the governing equation and boundary conditions, can serve to delineate the true behavior of the material in ultra small elastic structures, having very large surface-to-volume ratio. Now that the values of the material constants are available, a nanoscopic study of the Kelvin problem in second strain gradient theory is performed, and the result is compared quantitatively with those of the first strain gradient and traditional theories.
The elastic behavior of an edge dislocation, which is positioned outside of a nanoscale elliptical inhomogeneity, is studied within the interface elasticity approach incorporating the elastic moduli and surface tension of the interface. The complex potential function method is used. The dislocation stress field and the image force acting on the dislocation are found and analyzed in detail. The difference between the solutions obtained within the classical-elasticity and interface-elasticity approaches is discussed. It is shown that for the stress field, this difference can be significant in those points of the inhomogeneity-matrix interface, where the radius of curvature is smaller and which are closer to the dislocation. For the image force, this difference can be considerable or dispensable in dependence on the dislocation position, its Burgers vector orientation, and relations between the elastic moduli of the matrix, inhomogeneity and their interface. Under some special conditions, the dislocation can occupy a stable equilibrium position in atomically close vicinity of the interface. The size effect is demonstrated that the normalized image force strongly depends on the inhomogeneity size when it is in the range of several tens of nanometers, in contrast with the classical solution where this force is always constant. The general issue is that the interface elasticity effects become more evident when the characteristic sizes of the problem (inhomogeneity size, interface curvature radius and dislocation-interface spacing) reduce to the nanoscale.
Investigation of response of reinforced concrete (RC) structures due to axisymmetric macrocell corrosion of rebars is of concern after propagation of microcracks within the concrete medium. The geometry, boundary and interfaces conditions of the present problem are identical to those stated in part I. As seen in the companion paper, the exact solution to the boundary value problem corresponding to the uncracked steel-rust-concrete composite was possible. After appearance of the microcracks the concrete behavior becomes nonlinear anisotropic with post-cracking softening, and the associated problem is analytically intractable. Therefore, it is proposed to employ a novel meshless method, namely gradient reproducing kernel particle (GRKPM), in the cylindrical coordinates. The analytical and numerical solutions pertinent to the uncracked concrete are in good agreement. Subsequently, the effects of the parameters associated with the mechanical behavior of concrete and properties of rust on the time of surface cracking, the maximum values of consumed rebar per unit area of anode and crack width openings at the time of surface cracking, and the maximum value of radial stress at the rust-concrete interface are scrutinized in some detail.
Behavior of nanostructures, which are characterized by a large surface-to-volume ratio, is greatly influenced by their surface parameters, such as surface elastic moduli tensor. Accurate determination of the surface elastic constants by first principles is of particular interest. To this end, through consideration of the fundamental thermodynamic arguments for free solid surfaces, an analytical formulation for the change in specific Helmholtz surface free energy is developed. Relating this formulation to the corresponding energy calculated via first principles leads to the determination of the surface elastic moduli tensor. The surface mechanical properties, namely surface energy, surface stress, and surface elastic constants for Si(001) are all calculated for both cases of the reconstructed and ideal bulk terminated surface using ab initio method.
Assessment of the macrocell corrosion which deteriorates reinforced concrete (RC) structures have attracted the attention of many researchers during recent years. In this type of rebar corrosion, the reduction in cross-section of the rebar is significantly accelerated due to the large ratio of the cathode's area to the anode's area. In order to examine the problem, an analytical solution is proposed for prediction of the response of the RC structure from the time of steel depassivation to the stage just prior to the onset of microcrack propagation. To this end, a circular cylindrical RC member under axisymmetric macrocell corrosion of the reinforcement is considered. Both cases of the symmetric and asymmetric rebar corrosion along the length of the anode zone are studied. According to the experimentally observed data, corrosion products are modeled as a thin layer with a nonlinear stress-strain relation. The exact expressions of the elastic fields associated with the steel, and concrete media are obtained using Love's potential function. By imposing the boundary conditions, the resulting set of nonlinear equations are solved in each time step by Newton's method. The effects of the key parameters which have dominating role in the time of the onset of concrete cracking and maximum radial stress field of the concrete have been examined.
Carbon nanotubes (CNTs) are viewed as rolled graphene. Thus, an appropriate formulation describing the behavior of CNTs must contain the key information about both their initial configuration as graphene and final configuration as CNT. On this note, to date, some models, in particular based on the Cauchy-Born rule, for the description of CNTs behavior exist. A simplifying assumption in some of these models is that the length and perimeter of the CNT equal the corresponding dimensions of the unrolled initial configuration, thus neglecting the induced hoop and longitudinal strains. On the other hand, the present work offers a purely nonlinear continuum model suitable for the description of the large deformation of the graphene, without the need for the simplifying assumption and employment of the Cauchy-Born rule. The presented closed-form expressions for the Young's modulus and critical buckling strain of single-walled carbon nanotubes are functions of the elastic constants of the graphene, geometrical properties of the tube section, and a new material parameter that depends on the chirality angle; the new parameter is the coefficient of the introduced nonlinear term. The computed results are in good agreement with the available molecular mechanics results reported by different investigators.
The present paper addresses an analytical method to determine the electroelastic fields over a double-phase piezoelectric reinforcement interacting with an ellipsoidal single-inhomogeneity. The approach is based on the extension of the electro-mechanical equivalent inclusion method (EMEIM) to the piezoelectric double-inhomogeneity system. Accordingly, the double-inhomogeneity is replaced by an electroelastic double-inclusion problem with proper polynomial eigenstrains-electric fields. The long- and short-range interaction effects are intrinsically incorporated by the homogenizing eigenfields. The equivalent double-inclusion is subsequently decomposed to the single-inclusion problems by means of a superposition scheme. The methodology is further extended to the piezoelectric multi-inhomogeneity, where the particle core is surrounded by many layers of coatings of ellipsoidal shapes. Through consideration of various examples, including (1) 2D and 3D interaction problems of a coated piezoelectric reinforcement near a lamellar inhomogeneity and (2) a two-phase spherical particle with thick coating of variable thickness, the validity and robustness of the present theory are thoroughly demonstrated.
A meshless method called reproducing kernel particle method (RKPM) is exploited to cope with elastic-plastic fracture mechanics (EPFM) problems. The idea of arithmetic progression is assumed to place particles within the refinement zone in the vicinity of the crack tip. A comparison between two conventional treatments, visibility and diffraction, to crack discontinuity is conducted. Also, a tracking to find the appropriate diffraction parameter is performed. To assess the suggestions made, two mode I numerical simulations, pure tension and pure bending tests, are executed. Results including J integral, crack mouth opening displacement (CMOD), and plastic zone size and shape are compared with finite element method (FEM).
Behavior of a screw dislocation inside a nanotube (NT) is considered in the context of surface elasticity. The elastic fields as well as the image force acting over the dislocation are derived and analyzed in detail. In contrast with the result of classical elasticity, the screw dislocation is shown to be repelled by free surfaces and occupy two stable equilibrium positions near them. The image force strongly depends on the NT's inner and outer radii as well as surface elastic characteristics.
Consider a steel-rust-concrete composite consisting of a circular cylindrical concrete cover and a coaxial uniformly corroding steel reinforcement. Prediction of the amount of rust penetrated into the microcracks of concrete cover from a set of data measured at the surface of the concrete is of particular interest. The steel is assumed to be linear isotropic and rust follows a power law stress-strain relation. For the concrete, anisotropic behavior and post-cracking softening model is employed. The formulations lead to a nonlinear boundary value problem which is solved analytically. A key parameter β, defined as the ratio of the volume of corrosion products inside the cracks to the volume of the cracks, is calculated. With some efforts, this parameter is also extracted from the available theoretical and experimental studies for the purpose of comparison. The effects of the mechanical properties of rust and concrete on β is addressed.
The problem of edge dislocation inside the wall of a multi-walled nanotube accounting for the surface effects is addressed. Within the framework of surface elasticity the stress field is obtained, using complex potentials. Furthermore, the stress field and image forces acting on the dislocation, with and without an account of the surface stress, are compared together and discussed.
The axisymmetric problem of a concentric set of energetically consistent annular and penny-shaped cracks in an infinite piezoelectric body subjected to uniform far-field electromechanical loading is addressed. With the aid of a robust innovated technique, the pertinent four-part mixed boundary value problem (MBVP) is reduced to a decoupled Fredholm integral equation of the second kind. The results of two limiting cases of a single penny-shaped crack and a single annular crack are recovered. The contour plots of dimensionless intensity factors (IFs) at each crack front provide the stress and electric displacement intensity factors (SIFs and EDIFs, respectively) for all combination of crack sizes. The impermeable, permeable, and semipermeable models are also examined as limiting cases.
It is well-known that the conventional reproducing kernel particle method (RKPM) is unfavorable when dealing with the derivative type essential boundary conditions [1], [2], [3]. To remedy this issue a group of meshless methods in which the derivatives of a function can be incorporated in the formulation of the corresponding interpolation operator will be discussed. Formulation of generalized moving least squares (GMLS) on a domain and GMLS on a finite set of points will be presented. The generalized RKPM will be introduced as the discretized form of GMLS on a domain. Another method that helps to deal with derivative type essential boundary conditions is the gradient RKPM which incorporates the first gradients of the function in the reproducing equation. In present work the formulation of gradient RKPM will be derived in a more general framework. Some important properties of the shape functions for the group of methods under consideration are discussed. Moreover error estimates for the corresponding interpolants are derived. By generalizing the concept of corrected collocation method, it will be seen that in the case of employing each of the proposed methods to a BVP, not only the essential boundary conditions involving the function, but also the essential boundary conditions which involve the derivatives could be satisfied exactly at particles which are located on the boundary.
The effect of surface and interface elasticity in the analysis of the Saint-Venant torsion problem of an eccentrically two-phase fcc circular nanorod is considered; description of the behavior of such a small structure via usual classical theories cease to hold. In this work, the problem is formulated in the context of the surface/interface elasticity. For a rigorous solution of the proposed problem, conformal mapping with a Laurent series expansion are employed together. The numerical results well illustrate that the torsional rigidity and stress distribution corresponding to such nanosized structural elements are significantly affected by the size. In order to employ surface and interface elasticity, several key properties such as surface energy, surface stresses, and surface elastic constants of several fcc materials as well as interface properties of the noncoherent fcc bicrystals are derived in terms of Rafii-Tabar and Sutton interatomic potential function. For determination of the surface/interface parameters a molecular dynamics program, which uses the above-mentioned potential function, is developed. The calculated surface and interface properties are in reasonable agreement with the corresponding results in literature. Some applications of the given results can be contemplated in the design of micro-/nano-electromechanical systems.
One of the most crucial factors affecting the service life of reinforced concrete (RC) structures attacked by aggressive ions is reinforcement corrosion. As the steel corrosion progresses, crack propagation in concrete medium endangers the serviceability and the strength of RC structural members. In this study, a nonlinear mathematical model for determining the displacement and stress fields in RC structures subjected to reinforcement corrosion is introduced. For corrosion products, a nonlinear stress-strain relation which has been previously confirmed by experimental data is incorporated in the present analysis. In formulation of the governing equations for steel-rust-concrete composite, the rational behavior of corrosion products and penetration of rust into the microcracks are considered. An analytical approach as well as an innovative meshless method, gradient reproducing kernel particle method (GRKPM), are employed for solving the nonlinear boundary value problem. A reasonably good agreement between the results of the two methods is achieved. The performance of the proposed model is then investigated through various comparisons of predicted values with experimentally observed data, and again good agreement is obtained. Moreover, the effects of the crucial parameters associated with the mechanical behavior of rust and concrete on time to cover cracking and some measures of deterioration are studied for different values of rust penetration into the microcracks.
A new, robust homogenization scheme for determination of the effective properties of a periodic piezoelectric composite with general multi-coated inhomogeneities is developed. In this scheme the coating does not have to be thin, the shape and orientation of the inclusion and coatings do not have to be identical, their centers do not have to coincide, their properties do not have to remain uniform, and the microstructure can be with the 2D elliptic or the 3D ellipsoidal inclusions. The development starts from the local electromechanical equivalent inclusion principle through the introduction of the position-dependent equivalent eigenstrain and electric field. Then with a Fourier series expansion and a superposition procedure, the volume-averaged equivalent eigenstrain and electric field for each phase are obtained. The results in turn are used in an energy equivalent criterion to determine the effective properties of the composite. In this model the interphase interactions in each multi-coated particle and the long-range interactions between the periodically distributed particles are fully accounted for. To demonstrate its wide range of applicability, we applied it to examine the properties of several periodic composites: (i) piezoelectric PZT spherical particles in a polymer matrix, (ii) continuous glassy fibers with thin PZT coating in an epoxy matrix, (iii) spherical PZT particles coated by thick or functionally graded piezoelectric layer, (iv) spheroidal voids coated with a thick non-piezoelectric layer in a PZT matrix, and (v) spherical piezoelectric inhomogeneities with eccentric, non-uniform thickness coating. The calculated results reflect the complex nature of interplay between the properties of core, matrix, and coating, as well as whether the coating is uniform, functionally graded, or eccentric. The accuracy of this new scheme is checked against the double-inclusion and other micromechanics models, and good agreement is observed.
Propagation of P-wave in an unbounded elastic polymer medium which contains a set of nested concentric spherical piezoelectric inhomogeneities is formulated. The polymer matrix is made of Epoxy and is isotropic; each phase of the inhomogeneity is made of a different piezoelectric material and is radially polarized and has spherical isotropy. Note that the individual phases are homogeneous, and all interfaces are perfectly bonded. The scattered displacement and electric potentials in the matrix are expressed in terms of spherical wave vector functions and Legendre functions, respectively. The transmitted displacement and electric potentials within each phase of the piezoelectric particle are expressed in terms of Legendre functions. The equations of motion and electrostatics in each phase of the piezoelectric inhomogeneity lead to a system of coupled second order differential equations, which is solved using the generalized Frobenius series. The present theory is extended to the case where the core of the inhomogeneity is made of PZT-4 and its coating is made of functionally graded piezoelectric material (FGPM) whose microstructural composition varies smoothly from PZT-4 at the core-coating interface to Epoxy at the coating-matrix interface. The effects of different types of variation in the electro-mechanical properties of FGPM on scattering cross-section and other electro-mechanical fields are addressed. The present theory is valid for arbitrary coating thickness, and arbitrary frequencies.
An accurate numerical methodology for capturing the field quantities across the interfaces between material discontinuities, in the context of reproducing kernel particle method (RKPM), is of particular interest. For this purpose the innovative numerical technique, so-called augmented corrected collocation method is introduced; this technique is an extension of the corrected collocation method used for imposing essential boundary conditions (EBCs). The robustness of this methodology is shown by utilizing it to solve two benchmark problems of material discontinuities, namely the problem of circular inhomogeneity with uniform radial eigenstrain, and the problem of interaction between a crack and a circular inhomogeneity. Moreover, an efficient algorithm for computing the area associated to each particle for performing nodal quadrature in 2D in the context of RKPM is proposed. The efficacy of this algorithm in determination of the elastic fields within a plate weakened by a hole under uniform far-field tension is demonstrated. This algorithm combined with augmented corrected collocation method provides a powerful tool for treating problems with material discontinuities.
By virtue of a complete set of displacement potential functions and Hankel transform, the analytical expressions of Green's function of an exponentially graded elastic transversely isotropic half-space is presented. The given solution is analytically in exact agreement with the existing solution for a homogeneous transversely isotropic half-space. Employing a robust asymptotic decomposition technique, the Green's function is decomposed to the closed-form Green's function corresponding to the homogeneous transversely isotropic half-space and grading term with strong decaying integrands. This representation is very useful for numerical methods which are based on boundary-integral formulations such as boundary-element method since the numerically evaluated part is not responsible for the singularity. The high accuracy of the proposed numerical scheme is confirmed by some numerical examples.
The usual continuum theories are inadequate in predicting the mechanical behavior of solids in the presence of small defects and stress concentrators; it is well known that such continuum methods are unable to detect the change of the size of the inhomogeneities and defects. For these reasons various augmented continuum theories and strain gradient theories have been proposed in the literature. The major difficulty in implication of these theories lies in the lack of information about the additional material constants which appear in such theories. For fcc metals, for the calculation of the associated characteristic lengths which arise in first strain gradient theory, an atomistic approach based on the Sutton-Chen interatomic potential function is proposed. For the validity of the computed characteristic lengths, the phenomenon of the size effect pertinent to a nano-sized circular void within an fcc (111) plane is examined via both first strain gradient theory and lattice statics. Comparison of the results explains the physical ramifications of the characteristic lengths in improving the usual continuum results. Moreover, by reconsideration of the Kelvin problem it is shown that a commonly employed variant of the first strain gradient theory is only valid for a few fcc metals.
A screw dislocation outside an infinite cylindrical nano-inhomogeneity of circular cross section is considered within the isotropic theory of gradient elasticity. Fields of total displacements, elastic and plastic distortions, elastic strains and stresses are derived and analyzed in detail. In contrast with the case of classical elasticity, the gradient solutions are shown to possess no singularities at the dislocation line. Moreover, all stress components are continuous and smooth at the interface unlike the classical solution. As a result, the image force exerted on the dislocation due to the differences in elastic and gradient constants of the matrix and inhomogeneity, remains finite when the dislocation approaches the interface. The gradient solution demonstrates a non-classical size-effect in such a way that the stress level inside the inhomogeneity decreases with its size. The gradient and classical solutions coincide when the distances from the dislocation line and the interface exceed several atomic spacings.
The analytical treatment of an energetically consistent annular crack in a piezoelectric solid subjected to remote opening electromechanical loading is addressed. Potential functions and Hankel transform in combination with a robust technique are employed to reduce the solution of the mixed boundary value problem into a Fredholm integral equation of the second kind. The limiting case of a penny-shaped crack in a piezoelectric medium with energetically consistent boundary conditions over the crack faces is extracted for the first time. The electrical discharge phenomenon within the crack gap is modeled utilizing a non-linear constitutive law and the effects of the breakdown field on the energy release rate are delineated. The energy release rate, the electric displacement inside the crack gap, and the closing traction on crack faces are plotted for all possible geometries of a non-discharging annular crack.
Consider two piezoelectric ellipsoidal inhomogeneities of arbitrary size, orientation and material constants, which in turn are surrounded by an infinite isotropic medium. The system under consideration is subjected to far-field non-uniform electromechanical loadings. Based on the extension of the electromechanical equivalent inclusion method (EMEIM), the present paper develops a unified solution for determination of the associated electroelastic fields in the vicinity of interacting inhomogeneities. Accordingly, each of the piezoelectric inhomogeneities is broken down into two equivalent inclusions with proper polynomial eigenstrains and eigenelectric fields. The robustness and efficacy of the present solution are demonstrated through consideration of several boundary value problems. As a special case encompassed by the presented formulation, the interaction of a piezoelectric inhomogeneity and a lamellar inhomogeneity for two- and three-dimensional problems is addressed. For a particular case involving interaction of a slit-like crack and a piezoelectric circular fiber, comparison with the other available results in the literature attests to the validity of the proposed method. Subsequently, the effect of some parameters such as geometry and stiffness of each phase on the quantitative value of stress intensity factors (SIFs) are examined for far-field non-uniform loadings.
Consider an arbitrarily oriented ellipsoidal domain near the interface of an isotropic bimaterial space. It is assumed that a general class of piecewise nonuniform dilatational eigenstrain field is distributed within the ellipsoidal domain. Two theorems relevant to prediction of the nature of the induced displacement field for the interior and exterior points of the ellipsoidal domain are stated and proved. As a resultant the exact analytical expression of the elastic fields are obtained rigorously. In this work a new Eshelby-like tensor, A is introduced. In particular, the closed-form expressions for A associated with the interior points of spherical and cylindrical inclusion are derived. The stress field is presented for a single ellipsoidal inclusion which undergoes a Gaussian distribution of eigenstrain field and one of the principal axes of the domain is perpendicular to the interface. For the limiting case of spherical inclusion the closed-form solution is obtained and the associated strain energy is discussed. For further demonstration, two examples of two concentric spheres and three concentric cylinders with eigenstrain field distributions which are descriptive of the general class of functions defined in this paper. The effect of some parameters such as distance between the inclusion and the interface, and the ratio of the shear moduli of the two media on the induced elastic fields are examined.
The stress field of a multi-phase spherical / cylindrical inhomogeneity with arbitrary interface bonding conditions, subjected to both a uniform temperature change and a uniform hydrostatic tension, is presented. Imperfect bonding conditions are modeled using linear spring model and coherent interface model. In nanosize inhomogeneities, since the surface energy is not negligible with respect to the bulk energy, the effect of surface stresses is incorporated into the formulation. Accurate estimates for the thermal stresses of a functionally graded coated inhomogeneity with perfect and /~or imperfect interfaces are given. The influence of coating stiffness, coating thickness and interface conditions on the distribution of stress field is examined. It is observed that even a very thin coating has a prominent effect on stress distribution; hence, its exclusion from the model will lead to erroneous results.
Based on wave-function expansion, the time harmonic wave scattered by a circular and spherical inhomogeneity has been studied by numerous investigators. This method has also been employed to axisymmetrically coated circular and spherical inhomogeneities by some authors. When the geometry of the obstacle is not axisymmetric, the wave-function expansion is no longer applicable. In this paper, it is proposed to employ the dynamic equivalent inclusion method (DEIM) which is more general than the methods presented in the literature. It will be seen that DEIM may be used to treat a wide range of situations in a unified manner and is not bound to certain symmetries. The DEIM was first proposed by Fu and Mura [Fu, L.S., Mura, T., 1983. The determination of elastodynamic fields of an ellipsoidal inhomogeneity. ASME J. Appl. Mech. 50, 390-396], and no further developments have been done on it ever since. Its original formulation has some shortcomings with regard to the concept of homogenizing eigenstrains, and for usage of polynomial eigenstrains. Moreover, it is limited to single ellipsoidal inhomogeneity without coating. The new viewpoints of homogenizing eigenstress and eigenbody-force fields which are compatible with the physics of the problem are given. Expressing the eigenstress, eigenbody-force fields and the Green's function associated with the governing Helmholtz equation in terms of the spherical wave-functions is the natural choice and is very effective. Another important task is the development of the three dimensional DEIM for inhomogeneities having homogeneous or functionally graded (FG) coating with variable thickness, which eliminates any possible symmetries.
The axisymmetric contact problem of a rigid inclusion embedded in the piezoelectric bimaterial frictionless interface subjected to simultaneous far-field compression and electric displacement is addressed. With the aid of a robust technique, the coupled governing integral equations of this mixed boundary-value problem are reduced to decoupled Fredholm integral equations with a constraint equation. A useful limiting case for the contact problem of transversely isotropic bimaterials is addressed. The present solution is analytically in agreement with the existing solution for an isotropic bimaterial. Selected numerical results of interest to engineering applications including the radius of separation zone, contact pressure and contact electric displacement are plotted to portray the effects of precompression, piezoelectric coupling and material properties.
Meshless methods using kernel approximation like reproducing kernel particle method (RKPM) and gradient RKPM (GRKPM) generally use a set of particles to discretize the subjected domain. One of the major steps in discretization procedure is determination of associated volumes particles. In a non-uniform or irregular configuration of particles, determination of these volumes comprises some difficulties. This paper presents a straightforward numerical method for determination of related volumes and conducts a survey on influence of different assumption about computing the volume for each particle. Stress intensity factor (SIF) as a major representing parameter in fracture of solids is calculated by employing meshless methods for an edge-cracked plate under first mode loading condition which is one of the benchmark problems in fracture mechanics. The obtained results are compared using an analysis in terms of dilation parameter.
It is well-known that classical continuum theory has certain deficiencies in predicting material's behavior at the micro- and nanoscales, where the size effect is not negligible. Higher order continuum theories introduce new material constants into the formulation, making the interpretation of the size effect possible. One famous version of these theories is the couple stress theory, invoked to study the anti-plane problems of the elliptic inhomogeneities and inclusions in the present work. The formulation in elliptic coordinates leads to an exact series solution involving Mathieu functions. Subsequently, the elastic fields of a single inhomogeneity in conjunction with the Mori-Tanaka theory is employed to estimate the overall anti-plane shear moduli of composites with uni-directional elliptic cylindrical fibers. The dependence of the anti-plane elastic moduli on several important physical parameters such as size, aspect ratio and rigidity of the fiber, the characteristic length of the constituents, and the orientation of the reinforcements is analyzed. Based on the available data in the literature, certain nano-composite models have been proposed and their overall behavior estimated using the present theory.
The stress field of a screw dislocation inside an embedded nanowire is considered within the theory of strain-gradient elasticity. It is shown that the stress singularity is removed and all stress components are continuous and smooth across the interface, in contrast with the results obtained within the classical theory of elasticity. The maximum magnitude of dislocation stress depends greatly on the dislocation position, the nanowire size, and the ratios of shear moduli and gradient coefficients of the matrix and nanowire materials.
In composites, the stress intensity factors (SIFs) of a lamellar inhomogeneity near a multiphase reinforcement are of interest. Based on extension of Eshelby's equivalent inclusion method, a unified approach is presented to study the effect of a multiphase inhomogeneity on the SIF at the tip points of two- and three-dimensional lamellar inhomogeneities under nonuniform far-field loadings. Alteration of the SIF due to the presence of a coating layer around the inhomogeneity is addressed. Furthermore, the effect of geometry and stiffness of each phase of a multiphase reinforcement on the mixed mode SIFs of a lamellar inhomogeneity is investigated. In contrast to cracks whose SIFs are the same for uniaxial and multiaxial far-field loadings, all axial far-field applied stresses, which are parallel or perpendicular to the anticrack plane, result in the square root stress singularity at the anticrack tip points. However, only those components of the far-field shear stress whose couple vector is perpendicular to the anticrack plane would generate nonvanishing mixed mode SIFs, whereas for the shear components with couple vectors parallel to the anticrack plane, the SIF vanishes.
In contrast to the traditional study of composites containing ellipsoidal inclusions, we highlight some calculated results for the effective moduli when the inclusion shape can be described by the superspherical equation, , such that when p = 2 it reduces to a sphere and when p → ∞ it becomes a perfect cube. We consider the cases of both aligned and randomly oriented superspherical inclusions with isotropic, cubic, and transversely isotropic properties, and show how the shape parameter, p, affects the overall moduli of the composites during the spherical to cuboidal transition.
Due to inadequacy of the classical continuum theories at the nano-scale when dealing with defects, stress concentrators, and relevant deformation phenomena in solids, a refined approach that can capture the discrete atomic features of solids is essential. The inability to detect the size effect, giving unrealistically high values for some components of the stress field right on the edge of the stress concentrators, and infirmity to address the complex interaction between small inhomogeneities, cracks and as such when they are only a few nanometers apart, are among some of the drawbacks of the classical approach. An atomistic study which employs atomic finite element method in conjunction with the effective SC potential (AFEM-SC) is proposed as a remedy for treating the above-mentioned type of dilemmas. The stress distributions in presence of single and interacting stress concentrators are addressed, and for some cases the elastic modulus of the solid is calculated. Furthermore, for the first time a quantitative analysis accounting for a realistic atomic force law, rather than the simplistic uniform cohesive force law considered by Dugdale from the continuum viewpoint, is provided. By examination of the interacting cracks and the influence of the region of atomic forces interesting results are inferred. In the numerical examples Ag is considered merely to demonstrate the applicability of the present theory.
Consider a set of nested infinitely extended elastic cylindrical bodies possessing general cylindrical anisotropy embedded in an unbounded elastic isotropic medium. For general far-field loading, the nature of the elastic fields inside the inhomogeneities is predicted and a number of pertinent attractive properties is noted and proved. Moreover, the associated equivalent inclusion method (EIM) is concisely formulated. The concepts of the homogenization, spectral consistency conditions, and the so-called Eshelby-Fourier tensor are introduced. As a result the tedious and lengthy algebra encountered in the conventional EIM is circumvented and the corresponding large number of unknowns is reduced remarkably. Interestingly, the proposed theory is proved useful in the study of inhomogeneities with coatings made of functionally graded material (FGM). In addition to the relevance of the present work to multiple coated fiber reinforced composites, it is also of great value in the study of multi-shell quantum wire in electronic devices. The robustness and efficacy of the presented theories are demonstrated through consideration of several boundary value problems and various types of materials.
To date, the existing theories pertinent to the determination of the scattered fields of an inhomogeneity have been limited to certain topological symmetries for which the method of wave-function expansion is widely used. In the literature the wave-function expansion method has also been employed to the case involving concentric coated fiber. An alternative approach is the dynamic equivalent inclusion method (DEIM) proposed by Fu and Mura [L.S. Fu, T. Mura, The determination of elastodynamic fields of an ellipsoidal inhomogeneity. ASME J. Appl. Mech. 50 (1983) 390-396.] who found the scattered field of a single spheroidal inhomogeneity. The pioneering work of Eshelby [J.D. Eshelby, The determination of the elastic field of an ellipsoidal inclusion, and related problems, Proc. R. Soc. London, Ser. A A241 (1957) 376-396.] on elastostatic EIM is based on polynomial form of eigenstrains which holds certain useful properties and subsequently its application is only effective for certain relevant situations and not necessarily efficient for other problems. Nevertheless, Fu and Mura's analysis is also based on polynomial eigenstrains. It will be shown that taking the dynamic homogenizing eigenstrains in the form of the series expansion whose general term is products of functions of r and trigonometric functions of , is more rigorous and attractive for the problem under consideration. This natural form of solution gives very accurate result with just the first few terms of the series. Moreover, this work aims to extend the DEIM to the case of coated fiber obstacle with the rather complex topology where the coating-fiber phases are not concentric. The effect of variableness of the coating thickness on the elastodynamic fields is examined. Comparison with other analytical solutions, whenever available, establishes the remarkable accuracy and robustness of the proposed theory.
The stress fields of cylindrical and spherical multi-phase inhomogeneity systems with perfect or imperfect interfaces under uniform thermal and far-field mechanical loading conditions are investigated by use of the Boussinesq displacement potentials. The radius of the core inhomogeneity and the thickness of its surrounding coatings are arbitrary. The discontinuities in the tangential and normal components of the displacement at the imperfect interfaces are assumed to be proportional to the associated tractions. In this work, for the problems where the phases of the inhomogeneity system are homogeneous, the exact closed-form thermo-elastic solutions are presented. These solutions along with a systematic numerical methodology are utilized to solve various problems of physical importance, where the constituent phases of the inhomogeneity system may be made of a number of different functionally graded (FG) and homogeneous materials, and each interface may have a perfect or imperfect boundary condition, as desired. Also, the effect of the interfacial sliding and debonding on the stress field and elastic energy of an FG-coated inhomogeneity is examined.
A new meshless method called gradient reproducing kernel particle method (GRKPM) is proposed for numerical solutions of one-dimensional Burgers' equation with various values of viscosity and different initial and boundary conditions. Discretization is first done in the space via GRKPM, and subsequently, the reduced system of nonlinear ordinary differential equations is discretized in time by the Gear's method. Comparison with the exact solutions, which are only available for restricted initial conditions and values of viscosity, approves the efficacy of the proposed method. For challenging cases involving small viscosities, comparison with the results obtained using other numerical schemes in the literature further attests the desirable features of the presented methodology.
Displacement and strain fields of a screw dislocation in a nanowire are considered within the theory of gradient elasticity. The gradient solution of the corresponding boundary value problem is derived and discussed in detail. It is shown that the dislocation fields do not contain classical jumps and singularities at the dislocation line. The maximum values of the dislocation displacement and elastic strain strongly depend on both the dislocation position and nanowire radius, thus demonstrating a nonclassical size effect.
Gradient reproducing kernel particle method (GRKPM) is a meshless technique which incorporates the first gradients of the function into the reproducing equation of RKPM. Therefore, in two-dimensional space GRKPM introduces three types of shape functions rather than one. The robustness of GRKPM's shape functions is established by reconstruction of a third-order polynomial. To enforce the essential boundary conditions (EBCs), GRKPM's shape functions are modified by transformation technique. By utilizing the modified shape functions, the weak form of the nonlinear evolutionary Buckley-Leverett (BL) equation is discretized in space, rendering a system of nonlinear ordinary differential equations (ODEs). Subsequently, Gear's method is applied for temporal discretization of the ODEs. Through numerical experiments, employment of a moderate viscosity seeks the efficacy of the solution when the diffusion term is important; moreover, application of a small viscosity confirms the potential of the approach for treatment of the problems involving steep gradient regions. The outcomes are verified by performing convergence tests using uniformly spaced particles. Consideration of non-uniform distribution of particles further demonstrates the virtue of the presented methodology in producing smooth profiles in the critical regions near the fronts.
The propagation behavior of Love waves in a semi-infinite functionally graded piezoelectric material (FGPM) with a quadratic variation is addressed. The coupled electromechanical field equations are solved, and the dispersion relations, displacement, electric potential, and stress fields are obtained analytically for both electrically open and short conditions. The effects of gradient coefficient on phase velocity, group velocity, and electromechanical coupling factor are plotted and discussed. It is shown that the phase velocity associated with the non-piezoelectric case coincides with that of the corresponding piezoelectric material under electrically open conditions. Because of gradual variation in electromechanical properties, the initial stress during manufacturing process is negligible. Therefore, this model serves as an excellent substitute for the typical layered piezoelectric structures used in surface acoustic wave (SAW) devices. This work provides with a theoretical foundation for the design and practical applications of SAW devices with high performance.
The competition and interaction of two edge cracks within the triangular lattice of an fcc material are addressed. We have also examined the effect of presence of a nanovoid in the vicinity of one of the crack-tips, on the competition of the cracks. An atomic scale finite element method (AFEM) [B. Liu, Y. Huang, H. Jiang, S. Qu, K.C. Hwang, The atomic-scale finite element method, Comput. Methods Appl. Mech. Eng. 193 (2004) 1849-1864], based on the Morse interatomic potential, is employed to explore the events in the (1 1 1) plane. Particular attention is given to the phenomenon of brittle-to-ductile transition (BDT) that occurs during crack propagation.
This paper presents an innovative formulation of the RKPM (reproducing kernel particle method) pioneered by Liu. A major weakness of the conventional RKPM is in dealing with the derivative boundary conditions. The EFGM (element free Galerkin method) pioneered by Belytschko shares the same difficulty. The proposed RKPM referred to as GRKPM (gradient RKPM), incorporates the first gradients of the function in the reproducing equation. Therefore in three-dimensional space GRKPM consists of four independent types of shape functions. It is due to this feature that the corrected collocation method can be readily generalized and combined with GRKPM to enforce the EBCs (essential boundary conditions), involving both the field quantity and its first derivatives simultaneously. By considering several plate problems it is observed that GRKPM yields solutions of higher accuracy than those obtained using the conventional approach, while for a desired accuracy the number of particles needed in GRKPM is much less than in the traditional methodology.
Often, during fabrication processes of fiber-matrix composites, the pertinent interface may be made imperfectly bonded either deliberately or undesirably. The effect of electric capacitors and mechanical imperfections on the electro-mechanical fields associated with an anisotropic piezoelectric matrix containing a cylindrical inhomogeneity made of a different anisotropic piezoelectric material is of interest. In fact the interface imperfection condition presented in this paper is quite general, in the sense that any combination of mechanical and electrical imperfections may exist. The interface electrical imperfection is mimicked by the electric capacitors. The capacity of the capacitors is a measure of the electrical imperfection. The notion of complete electric barrier realizes when the capacity is equal to zero. For finite values of capacity, different electrical imperfections are modeled. When the capacity is infinitely large, perfect electrical interface reveals.
When a tensor-valued function σ(x)σ(x) is continuous in regions Σ0 and Σ1, but has a finite jump across the interface Γ01 between Σ0 and Σ1, then Γ01 is referred to as singular surface relative to the field σ(x)σ(x) . In this paper, it is intended to give a general treatment of three-dimensional static and free vibration analysis of bodies composed of multi-phase elastic and/or piezoelectric bodies with electro-mechanical singular surfaces. The geometry of the medium, boundary conditions, and the geometry of the singular surfaces may be arbitrary. The displacement field and the electric potential in each region are expressed in terms of functions composed of 3-D series and special 3-D functions. The composite functions are selected in such a way that they satisfy exactly: (1) the continuity of the displacement and the electric potential across the singular surfaces; and (2) the homogeneous and inhomogeneous kinematical boundary conditions. This methodology leads to remarkable accuracies in computation of the field quantities, including the quantities, which are discontinuous across the singular surfaces. Taking advantage of any symmetry that may be present in the problem, will substantially increase the convergence rate. For illustrations several examples are examined. Comparisons with the exact solutions, whenever available, established the remarkable accuracy and robustness of the present methodology.
Often, during fabrication of thin films on substrates, different types of defects may be introduced into the films. Recently, the determination of the elastic fields due to the self-assembly of quantum dots or strained islands in thin films has been of major concern. In the micromechanical studies, such strained islands are modeled by inclusions. This paper aims to develop a theory pertaining to the presence of nano-inclusions of various geometries within thin films having face centered cubic (fcc) structure. To this end, the notion of eigenstrain is combined with a many body inter-atomic potential suitable for fcc crystals. The interaction between atoms is modeled via Sutton-Chen (SC) potential. The displacements of the atoms are computed by employing the integral transform to the discretized equilibrium equation. Incorporation of the interaction between the inclusion and the free surface makes it feasible to investigate the effect of distance of the inclusion from the free surface. For the sake of comparison with the result from the continuum theory of elasticity, the problem of dislocation loop in an infinite domain is considered. Moreover, the behavior of the thin film in the presence of inclusion is studied using three-dimensional (3D) molecular dynamics (MD) simulation, and the result is compared with that obtained from the proposed theory. During the initial processes of introducing the inclusion into the film, the temperature is held at 0 K using a simple temperature scaling method. Afterwards, for the situations where thermal loading is of interest, the temperature is increased, and the pertinent thermo-mechanical fields are examined.
The examination of the effect of couple stresses on anti-plane electro-mechanical behaviour of piezoelectric media is of interest. The constitutive equations of piezoelectricity for a transversely isotropic piezoelectric medium of crystal class are derived in the context of couple stress elasticity. In this framework, a characteristic length appears in the formulation of anti-plane problems, by which examination of the size effect is possible. Also stemming from this approach is a new elasticity constant defined as the ratio of couple stress to the curvature, which based on the assumption of positive definiteness of the internal energy density, must be positive. For demonstration, this paper considers a piezoelectric-inhomogeneity system consisting of a circular piezoelectric inclusion or void inside an infinite body made of piezoelectric or solely elastic material. A special case pertinent to the circular piezoelectric inclusion embedded in a piezoelectric matrix, which was previously examined within the limitations of the classical piezoelectricity, is re-examined by the proposed theory. It is shown that the mechanical and electrical fields drastically depend on the relative size of the inhomogeneity with respect to the characteristic length of the material. The effects of couple stresses on the stress and electric concentrations are also addressed.
Consider a lamellar inhomogeneity embedded in an unbounded isotropic elastic medium. When the elastic moduli of the lamellar inhomogeneity are zero it is a crack, if its elastic moduli are infinite it is an anticrack, and when its elastic moduli are finite it is called a quasicrack. Based on the Eshelby's equivalent inclusion method (EIM), the present paper develops a unified approach for determination of the exact closed-form expressions for modes I, II, and III stress intensity factors (SIFs) at the tips of lamellar inhomogeneities under a remote applied polynomial loading.
The determination of the thermo-mechanical stress field in and around a spherical/cylindrical inhomogeneity surrounded by a functionally graded (FG) coating, which in turn is embedded in an infinite medium, is of interest. The present work, in the frame work of Boussinesq/Papkovich-Neuber displacement potentials method, discovers the potential functions by which not only the relevant boundary value problems (BVPs) in the literature, but also the more complex problem of the coated inhomogeneities with FG coating and sliding interfaces can be treated in a unified manner. The thermo-elastic fields pertinent to the inhomogeneities with multiple homogeneous coatings and various combinations of perfect/sliding interfaces can be computed exactly. Moreover, when the coatings are inhomogeneous, as long as the spatial variation of the thermo-elastic properties of the transition layer is describable by a piecewise continuous function with a finite number of jumps, an accurate solution can be obtained. The influence of interface conditions, stiffness of the core, spatial distributions of thermal expansion coefficient and shear modulus of FG coating, and loading condition on the stress field will be examined.
An exact thermoelasticity solution for a two-dimensional thick composite consisting of homogeneous and functionally graded layers is presented. The thermomechanical properties of functionally graded layers are assumed to vary exponentially through the thickness while the Poisson's ratio is taken to be constant. The heat transfer problem is solved under steady state condition accounting for the heat convection. Utilizing the stress function the governing equation reduces to a fourth order inhomogeneous partial differential equation which is solved exactly using Fourier series method. A comparative study is done between two sandwich structures with homogeneous and functionally graded coatings, respectively. The results reveal that stress concentration effects are eliminated and interfacial shear stress is reduced when a functionally graded coating is used.
The effective properties of elastic solids are strongly linked to their interacting micro-constituent phases. For materials containing dilute distributions of single-phase inhomogeneities, the overall behavior can be estimated in a straightforward manner. But in the non-dilute case, due to the complex inter-particle and particle-matrix interactions the treatment is rather involved. When the particles are heterogeneous, not only become the mentioned interactions more complex, but must properly account for the intra-particle interactions as well. The present work addresses an analytical approach to determine the overall moduli of elastic solids containing random distributions of arbitrarily oriented ellipsoidal heterogeneities at high concentrations. The approach is based on the extension of the equivalent inclusion method (EIM) to interacting multi-inhomogeneities. The long and short range interaction effects are intrinsically incorporated by the eigenstrain field. In the process, the average of the associated disturbance strain is computed within a representative volume element (RVE) using a superposition scheme. For verification of the proposed theory several theoretical estimates, experimental results, and bounds for the problems which have been obtained in the literature are reexamined. Consideration of more complex scenarios further demonstrates the efficacy of the proposed theory.
A major disadvantage of conventional meshless methods as compared to finite element method (FEM) is their weak performance in dealing with constraints. To overcome this difficulty, the penalty and Lagrange multiplier methods have been proposed in the literature. In the penalty method, constraints cannot be enforced exactly. On the other hand, the method of Lagrange multiplier leads to an ill-conditioned matrix which is not positive definite. The aim of this paper is to boost the effectiveness of the conventional reproducing kernel particle method (RKPM) in handling those types of constraints which specify the field variable and its gradient(s) conveniently. Insertion of the gradient term(s), along with generalization of the corrected collocation method, provides a breakthrough remedy in dealing with such controversial constraints. This methodology which is based on these concepts is referred to as gradient RKPM (GRKPM). Since one can easily relate to such types of constraints in the context of beam-columns and plates, some pertinent boundary value problems are analyzed. It is seen that GRKPM, not only enforces constraints and boundary conditions conveniently, but also leads to enhanced accuracy and substantial improvement of the convergence rate.
By virtue of a method of displacement potentials, an analytical treatment of the response of a transversely isotropic substrate-coating system subjected to axisymmetric time-harmonic excitations is presented. In determination of the corresponding elastic fields, infinite line integrals with singular complex kernels are encountered. Branch points, cuts, and poles along the path of integration are accounted for exactly, and the physical phenomena pertinent to wave propagation in the medium are also highlighted. For evaluation of the integrals at the singular points, an accurate analytical residual theory is presented. Comparisons with the existing numerical solutions for a two-layered transversely isotropic medium under static surface load, and a transversely isotropic half-space subjected to buried time-harmonic load are made to confirm the accuracy of the present solutions. Selected numerical results for displacements and stresses are presented to portray the dependence of the response of the substrate-coating system on the frequency of excitation and the role of coating layer.
Based on Hamilton's principle, a three-dimensional semianalytical method for the analysis of free vibration of a structure composed of piezoelectric and elastic materials is developed. Computations of dynamical behavior including natural frequencies, and mode shapes are of interest. In this approach, the mechanical displacement and electric potential functions, in each region, are expressed as products of a three-dimensional (3D) base function and a 3D polynomial with unknown coefficients. The base functions over every domain are constructed with respect to the kinematical boundary conditions, geometry of the structure, and the geometry of that domain. These base functions satisfy the necessary continuities in the displacement field and electric potential at the interfaces, and at the same time accounting for possible discontinuities in their derivatives at the interfaces. The mode shapes will be decomposed in accordance to the presence of any symmetry plane. The robustness of the proposed approach is demonstrated through comparison with the finite element method as applied to the following problems: (1) A perforated thick plate made of piezoelectric and elastic layers and (2) an elastic plate containing a hole, whose exact solution is available. For the latter problem, the result of the present study is in good agreement with the exact solution. Also, an example of a thick PZT plate containing an elastic inclusion with a complex interface, and various types of boundary conditions is considered.
A micromechanical approach for an accurate estimation of the effective moduli of composites reinforced with nondilute distribution of coated particles is developed. The theory is based on the extension of the equivalent inclusion method to interacting multiinhomogeneities. In this treatment the short and long range interactions of the reinforcing particles are appropriately incorporated through the homogenizing eigenstrain field. The periodicity of the microstructure of the medium suggests representing the eigenstrain field in terms of the Fourier series, accounting for the matrix-particle, interparticle, and intraparticle interactions with high precision. The proposed theory is valid for estimating the overall properties of solids containing thickly and/or functionally graded coated reinforcements. For demonstration, the problems of composites with body centered cubic (BCC) distribution of coated spherical particles as well as coated ellipsoidal particles are solved. The effect of volume fraction, coating thickness, coating stiffness, and shape and orientation of the coated ellipsoidal reinforcements on overall behavior of composites are thoroughly examined.
This paper is devoted to the study of scattering of plane harmonic waves by a piezoelectric sphere with spherical isotropy embedded in an unbounded isotropic polymer matrix. The scattered displacement field and the electric potential in the matrix are expressed in terms of spherical vector wave functions and spherical harmonic functions, respectively. For the field points inside the inhomogeneity, new displacement functions are introduced. Expansion of the new displacement functions and the electric potential in terms of spherical harmonic functions, the equations of motion and electrostatic lead to four second order ordinary differential equations (odes), where three of them are coupled. The coupled system of odes is solved by the generalized Frobenius series. This approach is readily used to handle low and high frequencies. Three different types of piezoelectric inhomogeneities, PZT-4, PZT-5H, and BaTiO3 are considered and the associated piezoelectric effects on the electro-mechanical fields, differential and total scattering cross-sections are addressed.
A thin coating made of linear elastic functionally graded material (FGM) perfectly bonded to an elastic substrate is considered. This work which is of particular interest to tribological community is devoted to the determination of the thermal and mechanical stresses due to mixed normal and tangential Hertzian surface pressure. The thermomechanical properties of the FGM coating are assumed to vary exponentially through the thickness. Solutions for temperature rise and stresses are obtained by use of Fourier transform technique. The influences of coating thickness, Peclet number and friction coefficient on temperature rise and stresses in the FGM coating are investigated. Comparative studies on FGM versus homogeneous surface coating under thermomechanical loading confirms that use of FGM coating could result in considerable reduction of surface temperature rise. The results also reveal that flexural tensile stresses in the FGM coating are significantly reduced.
This paper examines the electro-mechanical fields for a circular anisotropic piezoelectric fiber sensor inside an anisotropic piezoelectric or non-piezoelectric elastic matrix with imperfect interface under remote in-plane uniform tension. The interface imperfection is posed on the mechanical fields only. The present formulation admits different boundary value problems in a unified manner, so various fiber-matrix interface conditions are considered: (1) perfect bonding; (2) pure debonding; (3) in-plane pure sliding; (4) out-of-plane pure sliding; (5) full debonding; and (6) partial debonding. An interface condition is modeled by a specific layer of mechanical springs with vanishing thickness, namely ksd for normal debonding, kst for in-plane sliding, and ksv for out-of-plane sliding. Partial debonding is the one that allows to represent intermediate states between cases (1)-(5) above, for which the spring constants can take on any arbitrary values. An accurate three-dimensional approach in conjunction with an energy formulation based on linear theory of piezoelectricity is presented. The generalized displacement field is expressed in terms of series involving some appropriate amending functions. In the context of the present study the nature of the solution satisfies the necessary continuity in the electric potential across the fiber-matrix interface, while accounting for possible discontinuity in its derivative at the interface. This consideration accelerates the convergence rate significantly.
Molecular dynamics simulation method was employed to model mode I crack propagation in plates containing nanoscale clusters of impurities located in the vicinity of the crack tip. The plates and the clusters were considered to have an fcc structure. The interactions between the dissimilar atoms in the plates and clusters were modeled via the many-body Sutton-Chen inter-atomic potentials [Sutton, A.P., Chen, J., 1990. Long-range Finnis-Sinclair potentials. Philos. Mag. Lett. 61, 139-164], and their extended versions developed for fcc alloys by [Rafii-Tabar, H., Sutton, A.P., 1991. Long-range Finnis-Sinclair potentials for fcc metallic alloys. Philos. Mag. Lett. 63, 217-224]. In this paper, two different geometries for the clusters, in the form of a long strip and a cylinder, were considered, and their effects on the critical load and crack propagation were examined. Before reaching the critical load, the temperature of the system was held constant at 0 K by applying both a simple temperature scaling method and the Nose-Hoover thermostat [Rafii-Tabar, H., 2000. Modelling the nano-scale phenomena in condensed matter physics via computer-based numerical simulations. Phys. Rep. 325, 239-310]. The temperature was allowed to evolve, however, during all the subsequent stages of crack propagation. Velocity Verlet algorithm [Allen, M.P., Tildesley, D.J., 1987. Computer Simulation of Liquids, Clarendon Press] was employed to integrate the equations of motion.
The stress intensity factors (SIFs) for an arbitrarily oriented plane crack in the vicinity of a coated circular fiber is being sought. The method of solution is based on Shodja and Sarvestani's [1] equivalent inclusion method (EIM) for multi-inhomogeneity systems, which is an extension of Eshelby's [2] theory for a single ellipsoidal inhomogeneity. The proposed approach is very robust in the sense that it can effectively and systematically be applied to wide variety of fundamental problems, which are essential for micromechanical studies of composite materials, for example, see, Shodja et al. [3], Shodja and Roumi [4],[5].
Recently Shodja and Kamali [1], and Kamali and Shodja [2], introduced a 3D semi-analytical approach for determination of the electro-mechanical fields of piezoelectric solids with material singular surfaces. The proposed methodology is particularly effective for problems involving external and internal boundaries with complex geometries, which have closed form expressions, and not necessarily in the form of polynomials. The previous formulations are devoted to material singular surfaces with perfect bonding. Due to the promising features of the formulation, the authors have continued to study various capabilities as well as convergence rate and accuracy of the approach. The present work extends the formulation to solids in which the material discontinuity surfaces may have one of the following six conditions: (1) perfect bonding; (2) pure debonding; (3) in-plane pure sliding; (4) out-of-plane pure sliding; (5) full debonding; or (6) partial debonding. Moreover, the interface is electroded in the sense that the interface is subjected to an arbitrary electric potential function, Φ = f(x, y). One of the advantages of the proposed method is that all of the above-mentioned cases are treated in a unified manner.
A general three-dimensional semi-analytical solution of piezocomposite media consisting of various domains of distinct electro-mechanical properties is proposed. The interfaces between the domains may be non-planar. The geometry and boundary conditions may be arbitrary, and the applied loading can be in the form of traction, displacement, voltage, or any combination of them. In this approach, the unknown displacement field u1, u2, u3, and the electric potential Φ are taken as appropriate functions in each domain, such that the continuity of the displacement field and the electric potential are exactly satisfied at the interfaces. Also, the continuities of traction stresses and normal electric displacement across the interfaces are resolved with high accuracy. The homogeneous and non-homogeneous kinematic boundary conditions associated with the electric potential and the displacement field are incorporated at the boundaries exactly.
When applying the equivalent inclusion method (EIM) to a composite material with non-dilute distribution of reinforcement particles, due to the complex interaction between the particles, the homogenizing eigenstrain field will in general be highly nonlinear. The interaction becomes more complex, when the reinforcements are multi-phase particles, i.e., the core inhomogeneity is surrounded by many layers of coatings. In this paper, a treatment for an accurate determination of the distribution of homogenizing eigenstrain fields corresponding to composites with non-dilute periodic distribution of multi-phase reinforcement particles is given. The proposed method is applicable to problems, where the reinforcement particles have: very thick coatings; functionally graded (FG) coatings; or coatings with variable thicknesses. Strong dependence of the overall response of composites on the microstructure of their reinforcement particles is well recognized. The theory is extended to estimate the effective elastic moduli of such composites.
In this paper, an accurate series solution in conjunction with an energy formulation for the treatment of piezocomposite plates with arbitrary geometry and aspect ratio, under both electrical and mechanical loadings are proposed. A remedy for dealing with nonhomogeneous boundary conditions is also presented. Through introduction of amending polynomials of order pk for the kth layer, the accuracy and convergence rate are dramatically improved. These polynomials ensure continuity of the generalized displacement fields across the interfaces, while their derivatives can have the required discontinuities up to a desired order. Moreover, depending on the nature of the physical problem under consideration, incorporation of the appropriate functions result in greater convergence rate and precision of the solution.
Based on the Eshelby's equivalent inclusion method (EIM) and Hill's theorem on discontinuities of elastic fields across the interfaces, a theory for the determination of the stress intensity factors (SIFs) of arbitrarily oriented interacting cracks under non-uniform far-field applied stress (strain) is developed. As shown in this investigation the EIM proposed by Moschovidis and Mura can be extended for treatment of such problems, but their formulations are quite cumbersome and computationally inefficient. An alternative analytical approach is proposed that is computationally more efficient, and unlike the method of Moschovidis and Mura can easily handle complex problems of interacting inhomogeneities and cracks. It is seen that as the interaction between the inhomogeneities becomes stronger, this method yields results that are closer to the solutions reported in the literature than the solutions obtained using the extended EIM of Moschovidis and Mura, which is developed herein. Problems involving combinations of interacting elliptic and penny shape cracks and inhomogeneities are excellent candidates for demonstration of the accuracy and robustness of the present theory, for which the previous EIM produces less accurate results. Due to the limitations imposed on the existing methods, every reported treatment has been tailored for a certain category of problems, and only uniform far-field loadings have been remedied. In contrast, the present theory is more general than the previously reported theories and it encompasses interacting cracks having a variety of geometries subjected to non-uniform far-field applied stress (strain); moreover, it is applicable to modes, I, II, III, and mixed mode fracture.
The evolution of the microstructure of an assembly of cohesionless granular materials with associated pores, which carry the overall applied stresses through frictional contacts is a complex phenomenon. The macroscopic flow of such materials take place by the virtue of the relative rolling and sliding of the grains on the micro-scale. A new discrete element method for biaxial compression simulations of random assemblies of oval particles with mixed sizes is introduced. During the course of deformation, the new positions of the grains are determined by employing the static equilibrium equations. A key aspect of the method is that, it is formulated for ellipse cross-sectional particles, hence desirable inherent anisotropies are possible. A robust algorithm for the determination of the contact points between neighbouring grains is given. Employing the present methodology, many aspects of the behaviour of two-dimensional assemblies of oval cross-sectional rods have been successfully addressed. The effects of initial void ratio, interparticle friction angle, aspect ratio, and bedding angle on the rolling and sliding contacts are examined. The distribution of normals to the rolling and sliding contacts have different patterns and are concentrated along directions, which are approximately perpendicular to one another. On the other hand, the distribution of all contact normals (combined rolling and sliding) are close to that of rolling contacts, which confirm that rolling is the dominant mechanism. This phenomenon becomes more pronounced for higher intergranular friction angle. Characteristics of the rolling and sliding contacts are also discussed in the context of the force angle, which is the inclination of contact force with respect to the contact normal. Copyright © 2003 John Wiley & Sons, Ltd.
Consider a double-inhomogeneity system whose microstructural configuration is composed of an ellipsoidal inhomogeneity of arbitrary elastic constants, size, and orientation encapsulated in another ellipsoidal inhomogeneity, which in turn is surrounded by an infinite medium. Each of these three constituents in general possesses elastic constants different from one another. The double-inhomogeneity system under consideration is subjected to far-field strain (stress). Using the equivalent inclusion method (EIM), the double inhomogeneity is replaced by an equivalent double-inclusion (EDI) problem with proper polynomial eigenstrains. The double inclusion is subsequently broken down to single-inclusion problems by means of superposition. The present theory is the first to obtain the actual distribution rather than the averages of the field quantities over the double inhomogeneity using Eshelby's EIM. The present method is precise and is valid for thin as well as thick layers of coatings, and accommodates eccentric heterogeneity of arbitrary size and orientation. To establish the accuracy and robustness of the present method and for the sake of comparison, results on some of the previously reported problems, which are special cases encompassed by the present theory, will be re-examined. The formulations are easily extended to treat multi-inhomogeneity cases, where an inhomogeneity is surrounded by many layers of coatings. Employing an averaging scheme to the present theory, the average consistency conditions reported by Hori and Nemat-Nasser for the evaluation of average strains and stresses are recovered.
The present review on inclusion problems emphasizes papers primarily published after 1982. Materials associated with inclusions are composite materials, precipitated or transformed alloys, porous media, and polycrystals. The inclusion problems deal with the following subjects of these materials: (1) stress fields caused by non-elastic strains (eigenstrains) and; (2) stress disturbances due to heterogeneity and inhomogeneities of materials under applied stresses; (3) average elastic moduli and average thermal properties; (4) nonelastic constitutive equations; (5) behavior of inclusions including nucleation, growth, and collapse of voids; (6) cracks and inclusions including the transformation toughening, crack growth through composites and stress intensity factors; (7) sliding and debonding inclusions; and (8) dynamic effects of inclusions. The present review is an update to the review paper, which appeared in Applied Mechanics Reviews, Volume 41 (1988), and includes opinions of some of the experts who made significant contributions to the field of inclusion problems. It is our hope that we cited all the important papers relevant to the subject of inclusion problems. The first author would welcome anyone's comments and any references which were not included in this review.
Thin-film interconnects subjected to combined thermomechanical fatigue (TMF) and corrosion are considered. Thin-films are composed of polycrystalline materials, and grain boundaries (GBs) have a critical role in the deformation and failure of such materials. Intergranular void formation in a thin metal conductor occurs as a result of both electro-migration and stress-induced diffusion. In our theoretical model, the presence of voids in the interconnect serve as a potential site for corrosion fatigue cracking (CFC), where hydrogen diffusion occurs under a hydrostatic stress field near crack tips or notch roots and hydrogen concentration reaches a saturated value at notch tips. In effect the presence of hydrogen atoms decreases the surface energy of the film, which in turn causes crack initiation in front of the notch root. We consider that the formation of persistent slip bands (PSBs), which are narrow bands of highly localized cyclic strain is the mechanism of fatigue crack initiation along the GBs. We give a new expression for the Gibbs free energy change, which accounts for the reduction of the surface energy of metal film with cumulative increment of hydrogen intruded into the film. The micromechanically based governing equations consist of an advection-diffusion equation, which explains the time evolution of hydrogen concentration is coupled with the singular integral equation for the dislocation density distribution. The multiple scale reproducing kernel particle method (RKPM) in conjunction with multiresolution analysis provide us with a powerful tool for solving the governing evolutionary partial differential equation (PDE). The integral equation is a Fredholm type of the first kind with generalized Cauchy kernel and a bounded Fredholm kernel. We will solve the coupled advection-diffusion equation and the singular integral equation by simultaneous application of the RKPM and a Gauss-Jacobi integration technique, respectively.
Apart from crack closure which has been employed extensively to explain apparent differences in the behaviour of short and long cracks, dislocation crack tip shielding is investigated as an additional contributing factor. The double slip plane (DSP) crack model is employed and a numerical approach is followed for the calculation of the dislocation density distributions on the crack and the slip planes and the plastic zone size. By accounting for dislocation crack tip shielding, the critical stress σcr and applied stress intensity factor KA,cr which define the onset of crack advance, exhibit a crack length dependence which is a manifestation of the anomalous short crack behaviour. It is shown, that below a critical crack length KA,cr is not constant, but rather decreases with decreasing crack length. Furthermore, a critical stress smaller than that predicted by linear elastic fracture mechanics is found. A method to calculate crack propagation rates based on dislocation density distributions is also presented. It is shown that under cyclic loading, a short crack propagates below the threshold stress intensity of a long crack and exhibits faster crack growth rates for the same nominal crack driving force. For the mild crack growth regime, Paris power-law exponents of 2 and 2.7 are predicted, depending on the value of an adjustable parameter in the configuration of the DSP model.
A disclination dipole wall model of grain boundaries incorporating a dislocation emission mechanism has been developed. Uniform and non-uniform disclination spacings have been treated, and the complete stress field equations have been solved for the uniform case. Two models of dislocation emission from the disclination dipoles are considered as plastic deformation mechanisms. A stable grain boundary with limited plastic deformation potential is described.
Traditionally, sedimentation and self-weight consolidation have been viewed as physically distinct processes requiring separate treatment. Relatively recently, Pane and Schiffman1 and also Philip and Smiles2 have suggested that the two processes may be described by a single partial differential equation, essentially that of Gibson et al.3 The former suggests a modification of Terzaghi's effective stress principle while the paper by Philip and Smiles suggests that a suitable modelling of material properties is sufficient. We have adopted the latter approach by allowing for the compressibility of the material in question to change abruptly from finite values to infinity in the so-called transition region which delineates that portion of space where effective stress is zero from that where effective stress in non-zero. This procedure gives rise to serious difficulties when trying to solve the governing partial differential equation numerically. These difficulties are circumvented by using a relatively new numerical technique known as the Moving Finite Element (MFE) method. The MFE method is especially effective in solving problems having solutions that characteristically exhibit shock-like structure. The modelling of sedimentation and self-weight consolidation from a single governing model is an ideal candidate for MFE due to the abrupt, almost discontinuous change in void ratio displayed in the transition region.
A system of evolutionary partial differential equations (PDEs) describing the two-phase flow of immiscible fluids in one dimension is developed. In this formulation, the wetting and nonwetting phases are treated to be incompressible and compressible, respectively. This treatment is indeed necessary when a compressible nonwetting phase is subjected to compression during confinement. The system of PDEs consists of an evolution equation for the wetting-phase saturation and an evolution equation for the pressure in the nonwetting phase. This system is applied to the problem of unsaturated flows to assess the importance of air-phase compressibility. For those situations where air can move freely within the medium and ultimately escape through the boundaries without experiencing any compression, it is then reasonable to treat air as an incompressible phase so that the total volumetric flux becomes spatially invariant. As shown by Morel-Seytoux and Billica, this leads to a coupled evolution equation for water saturation and an integral expression for total volumetric flux. In the event that an air phase is subjected to confinement in some manner, the total volumetric flux cannot be assumed to be spatially invariant as did Morel-Seytouxet al. The system of evolutionary PDEs developed in the present paper are precise and uniformly valid in time and space and, more importantly, smoothly accommodate a nonwetting phase whose state may change from unconfined to confined during the course of the flow process and vice-versa. Consequently, the complete system of PDEs may be used to analyze unsaturated flows in a straightforward manner. Depending on the initial and boundary conditions, the solutions to the system of PDEs may develop steep gradients near the wetting front. For this reason, the moving finite element (MFE) method introduced by Miller and Miller in conjunction with Gear's implicit stiff temporal solver provides an automatic and powerful scheme suitable for the initial-boundary value-problem (IBVP) developed herein.
In order to establish guidelines for modeling the macroscopic behavior of granular materials, an experimental study of the evolution of the microstructure of an assembly of granular materials under a uniform confining pressure and subjected to a pure shear was conducted. The granular material used in the study consisted of photoelastically sensitive rod-shaped particles of oval cross-sections. It was found that (i) the distribution of branches and contact normals are almost identical, (ii) the second rank fabric tensor does not adequately describe the microstructure of highly anisotropic samples, (iii) the density of contacts whose normals lie along the major and minor principal stress axes, varies sharply initially and then approaches a constant value in the course of deformation, and (iv) the density of contacts with planes parallel to the maximum shear stress plane remains practically constant throughout the deformation.
One end of a long, naturally curved elastic sheet is clamped onto an inclined plane. The other end is acted on by a constant vertical force which tends to open the curved sheet. This nonlinear large deflection problem is studied by series perturbation, numerical integration and exact analytic solution. The occurrence of roll-up depends on the angle of the inclined plane an a nondimensional parameter representing the importance of curvature and flexural rigidity to that of the end load.









Mohammad Taher Kamali
Current: Associate Professor at University of Hormozgan, Hormozgan, Iran
Email: kamali@hormozgan.ac.ir
Babak Shokrolahi-Zadeh
Current: Assistant Professor at University of Hormozgan, Hormozgan, Iran
Email: shokrolahi-zadeh@hormozgan.ac.ir
Keivan Kiani
Current: Associate Professor, Department of Civil Engineering, K.N. Toosi University of Technology
Email: k_kiani@kntu.ac.ir, keivankiani@yahoo.com
Maryam Tabatabaei
Current: Postdoctoral Scholar, Pennsylvania State University
Email: smt366@psu.edu
Roohollah Hashemi
Farzaneh Ojaghnezhad
Current: Assistant Professor, Alzahra University, Tehran, Iran
Email: f.ojaghnezhad@alzahra.ac.ir
Morteza Eskandari
Current: Assistant Professor, Department of Civil Engineering, Sharif University of Technology
Email: eskandari@sharif.edu
Mohammad Rasoul Delfani
Current: Assistant Professor of Civil Engineering at K. N. Toosi University of Technology
Email: delfani@kntu.ac.ir
Azadeh Goodarzi
Ehsan Rashidinejad
Current: post-doctoral grant recipient at Ghent University,Ghent, Belgium
Email: ehsan.rashidinejad@ugent.be
Camelia Enzevaee
Current: Postdoctoral Researcher at Sharif University of Technology
Email: cenzevaee@gmail.com
Alireza Sarvestani
Current: Assistant professor, Mercur University, Macon, Gorgia
Email: sarvestani_a@mercer.edu
Alireza Hashemian
Reza Soheilifard
Current: Assistant Professor at University of Hakim Sabzevari, Iran
Email: r.soheilifard@hsu.ac.ir
Arash Dahi Taleghani
Current: Associate professor of petroleum engineering at Pennsylvania State University
Email: arash.dahi@psu.edu
Ali Ghahremaninezhad
Current: Associate Professor, University of Maiami
Email: a.ghahremani@miami.edu
Ladan Pahlevani
Hamed Hatami-Marbini
Current: Associate Professor at University of Illinois at Chicago
Email: Hatami@uic.edu
Farzaneh Ojaghnezhad
Current: Assistant Professor, Alzahra University, Tehran, Iran
Email: f.ojaghnezhad@alzahra.ac.ir
Maryam Tabatabaei
Current: Postdoctoral Scholar, Pennsylvania State University
Email: smt366@psu.edu
Maryam Ghazisaeidi
Current: Associate Professor at The Ohio State University
Email: ghazisaeidi.1@osu.edu
Morteza Eskandari
Current: Assistant Professor, Department of Civil Engineering, Sharif University of Technology
Email: eskandari@sharif.edu
Mohammad Rasoul Delfani
Current: Assistant Professor of Civil Engineering at K. N. Toosi University of Technology
Email: delfani@kntu.ac.ir
Kamyar Davoudi
Current: Postdoctoral fellow in the Harvard School of Engineering and Applied Sciences
Vahid Keshavarzzadeh
Current: Postdoctoral Fellow in the Scientific Computing and Imaging Institute at the University of Utah
Email: vkeshava@sci.utah.edu
Hamed Haftbaradaran
Current: Assistant Professor, University of Isfahan, Isfahan, Iran
Email: h.haftbaradaran@eng.ui.ac.ir
Mani Khezri
Current: Lecturer of Structural Engineering, University of Sydney
Email: mani.khezri@sydney.edu.au
Azadeh Goodarzi
Mohammad Mashayekhi
Current: Ph.D. student at Sharif University of Technology
Email: mashayekhimohammad23@gmail.com
Ehsan Rashidinejad
Current: post-doctoral grant recipient at Ghent University,Ghent, Belgium
Email: ehsan.rashidinejad@ugent.be
Fatemeh Ahmadpoor
Current: Assistant Professor at NJIT, Mechanical and Industrial Engr
Email: fatemeh.ahmadpoor@njit.edu
Reza Namakian
Current: PhD Candidate at Louisiana State University
Email: r.namakian@gmail.com
Leila Malekmotiei
Current: Visiting Assistant Professor at Villanova University
Email: lmalek1@lsu.edu
Hossein Ahmadzadeh-Bakhshayesh
Current: Associate Consultant at Exponent Mechanical Engineering Practice
Email: hsn.ahmadzadeh@gmail.com
Aref Samadi-Dooki
Current: Mechanical Engineering Consultant at DuPont
Email: arefsamadi@gmail.com
Shaghayegh Rezazadeh Kalehbasti
Current: Researcher at Brown University; PhD in Solid Mechanics
Email: rezaz004@umn.edu
Camelia Enzevaee
Current: Postdoctoral Researcher at Sharif University of Technology
Email: cenzevaee@gmail.com
Behnaz Bahari
Mahmood Esmaeeli
Current: PhD student at Sharif University of Technology
Email: s.mahmood_sh@yahoo.com
Hashem Moosavian
Current: PhD student at Sharif University of Technology
Email: hashemmoosavian@yahoo.com
Azadeh Etehadieh-koochak
Micromechanics of Defects in Solids
Strength of Materials I & II
Advanced Strength of Materials
Fracture Mechanics
Dislocation Based Fracture Mechanics
Mechanics of Continuous Media
Theory of Elasticity I & II
Advanced Engineering Mathematics
Topics in Applied Mathematics
Wave Propagation in Elastic Solids